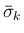
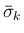 は、
は、
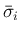 と
と 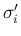 は同符号、
は同符号、
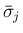 と
と 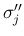 は同符号となる。
よって
は同符号となる。
よって
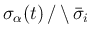 かどうかは、
かどうかは、
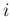 -特性族の真性非線形性や
-特性族の真性非線形性や 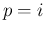 かどうかに関わらず、
かどうかに関わらず、
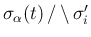 かどうかに一致する。
かどうかに一致する。
よって、いずれも approach するなら
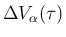 の
の
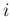 -特性族の項は
-特性族の項は
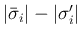 となり、
いずれも approach しなければ
となり、
いずれも approach しなければ 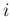 -特性族の項はない。
-特性族の項はない。
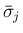 ,
, 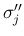 についても同様であり、
についても同様であり、
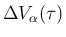 には
には
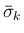 ,
, 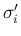 ,
, 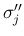 以外の項は含まれないので、いずれの場合も、
以外の項は含まれないので、いずれの場合も、
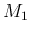 は Lemman 7.2 (i), (iii), (iv) の
は Lemman 7.2 (i), (iii), (iv) の 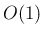 の部分、
および Lemma 7.2 (ii) の
の部分、
および Lemma 7.2 (ii) の
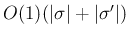 の部分を押さえる
定数であることに注意する (3.2 節、
3.3 節参照)。
の部分を押さえる
定数であることに注意する (3.2 節、
3.3 節参照)。
竹野茂治@新潟工科大学