しかし、![]() ,
, ![]() が十分近ければ、
その解が今まで紹介した単純波で構成できることが知られている
([5])。
が十分近ければ、
その解が今まで紹介した単純波で構成できることが知られている
([5])。
双曲型保存則方程式 (5.1) の
すべての ![]() -特性方向が、
-特性方向が、
![]() 内で真性非線形であるか、または線形退化である場合、
内で真性非線形であるか、または線形退化である場合、
![]() 内の各
内の各 ![]() に対し、
に対し、
![]() を含む十分小さい近傍
を含む十分小さい近傍 ![]() (
(![]() ) をとれば、
この
) をとれば、
この ![]() 内の任意の
内の任意の ![]() ,
, ![]() に対して、
リーマン問題 (5.2) の解は、
原点を出発する高々
に対して、
リーマン問題 (5.2) の解は、
原点を出発する高々 ![]() 個の単純波 (膨張波、衝撃波、接触不連続) と、
それにはさまれる高々
個の単純波 (膨張波、衝撃波、接触不連続) と、
それにはさまれる高々 ![]() 個の定数ベクトル
(一番左と一番右は
個の定数ベクトル
(一番左と一番右は ![]() ,
, ![]() ) によって構成できる。
) によって構成できる。
この定理は、後で説明するように気体の例の場合は
具体的に解を構成する手順を与えられるし、
![]() と
と ![]() が近くない場合でも解が求められる場合もあるが、
一般の方程式 (5.1) の場合は
陰関数定理によって十分近くの
が近くない場合でも解が求められる場合もあるが、
一般の方程式 (5.1) の場合は
陰関数定理によって十分近くの ![]() ,
, ![]() に対して
解の存在が示せるにすぎず、
具体的に構成するのも難しい。
しかし少なくともそのような
に対して
解の存在が示せるにすぎず、
具体的に構成するのも難しい。
しかし少なくともそのような ![]() ,
, ![]() に対して
必ずその形で
に対して
必ずその形で ![]() から
から ![]() へ単純波をつないで
解を作ることができることが保証される。
へ単純波をつないで
解を作ることができることが保証される。
証明
![]() -特性方向が真性非線形である場合は、
命題 5.1 の証明にある
-特性方向が真性非線形である場合は、
命題 5.1 の証明にある
![]() を
を
![]() と書くこととし
(
と書くこととし
(![]() のときは膨張波の右に現われるベクトル、
のときは膨張波の右に現われるベクトル、
![]() のときは衝撃波の右に現われるベクトル)、
のときは衝撃波の右に現われるベクトル)、
![]() -特性方向が線形退化である場合は、
-特性方向が線形退化である場合は、
![]() を
を
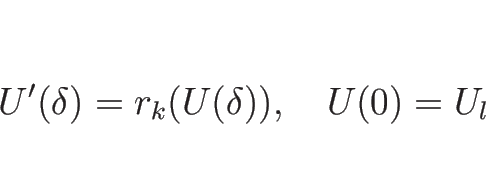
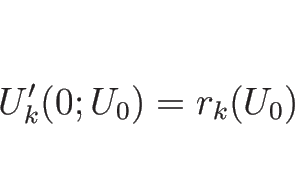
このとき、
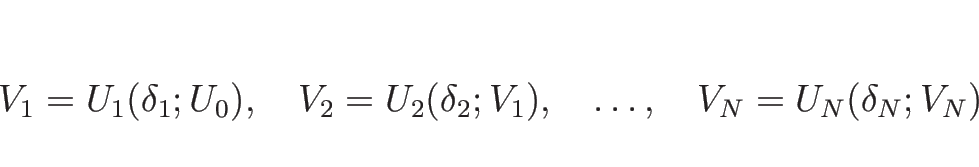
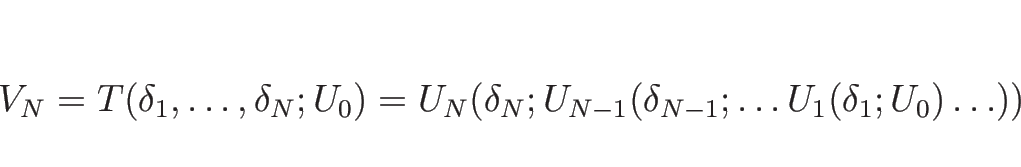
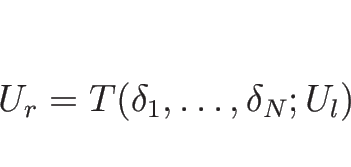
![]() なので、
なので、
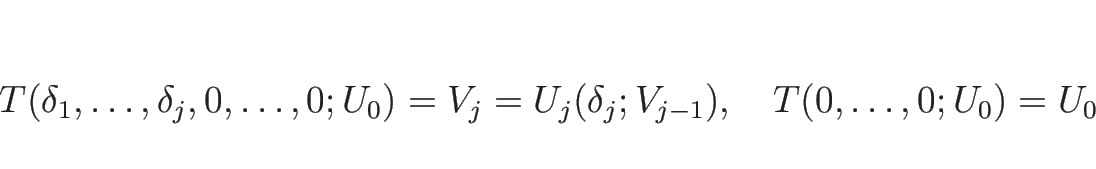
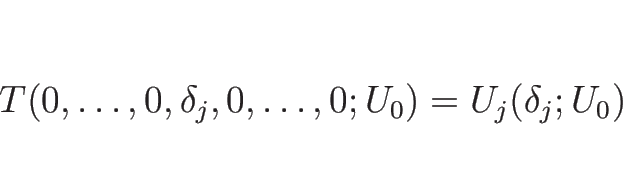
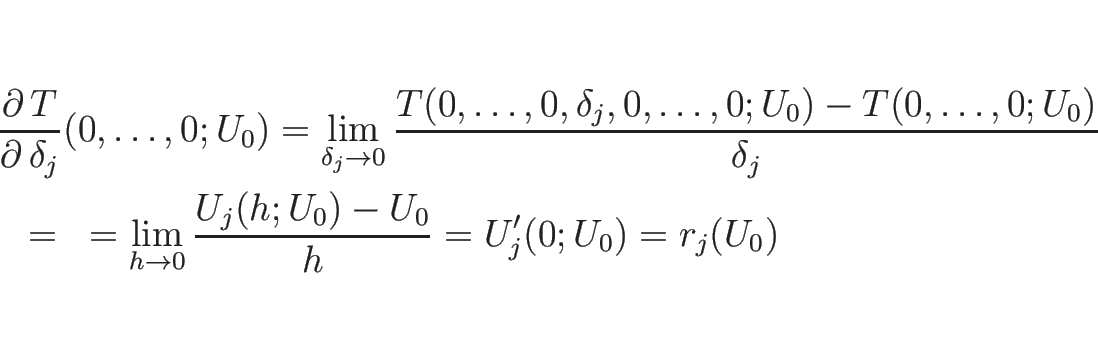
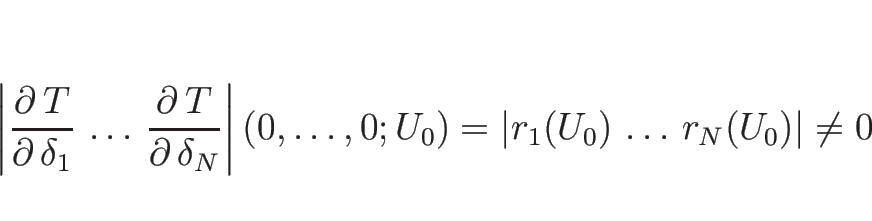
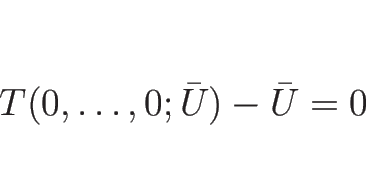
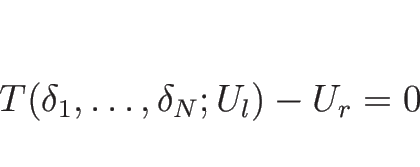
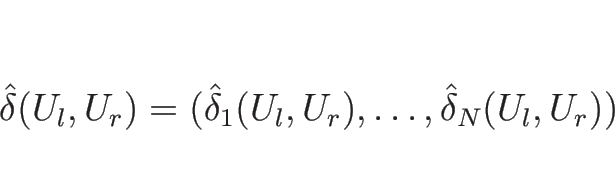
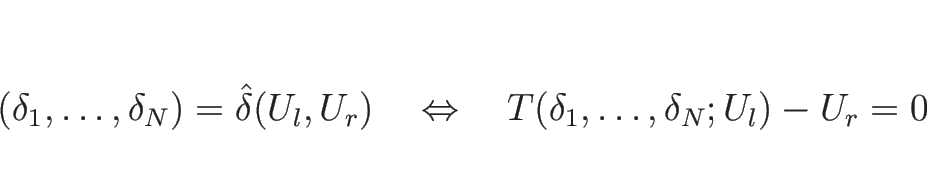
これにより、![]() から
から ![]() までを
までを
![]() (
(![]() ,
, ![]() ,
, ![]() ) によって単純波と定数ベクトルで
つなぐことができ、それによって
リーマン問題 (5.2) の解を構成できる。
) によって単純波と定数ベクトルで
つなぐことができ、それによって
リーマン問題 (5.2) の解を構成できる。
5.2 節の内容、 およびこの定理の証明は、単にリーマン問題の解の存在だけではなく、 このような形の解が一意的に決まることも示している。
竹野茂治@新潟工科大学