![\includegraphics[height=0.2\textheight]{Riemann1.eps}](img976.png)
|
このように同じ点を出発する場合、
それらの波は同じ特性方向の波は 1 つしかなく、
左から 1,2,...,![]() という順の特性方向の波しか並び得ないことを
以下に見てみる。
という順の特性方向の波しか並び得ないことを
以下に見てみる。
まず、定数ベクトルを挟んで、その左に ![]() -膨張波、
右に
-膨張波、
右に ![]() -衝撃波がある場合を考える (図 5.2)。
-衝撃波がある場合を考える (図 5.2)。
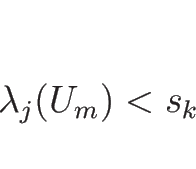
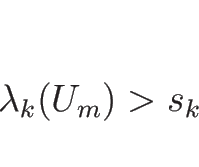
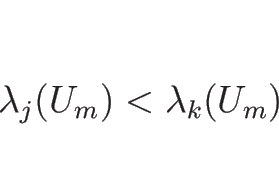
なお、この ![]() -衝撃波が
-衝撃波が ![]() -接触不連続である場合も、ラックス条件の代わりに
-接触不連続である場合も、ラックス条件の代わりに
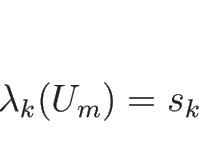
![]() -衝撃波の右に
-衝撃波の右に ![]() -膨張波がある場合
(図 5.3) は、
-膨張波がある場合
(図 5.3) は、
![]() であるが、ラックス条件により
であるが、ラックス条件により
![]() となるので
となるので
![]() となるので、やはり
となるので、やはり ![]() となる。
この
となる。
この ![]() -衝撃波が
-衝撃波が ![]() -接触不連続である場合も、
ラックス条件の代わりに
-接触不連続である場合も、
ラックス条件の代わりに
![]() となるので、やはり
となるので、やはり
![]() となるので
となるので
![]() が言える。
が言える。
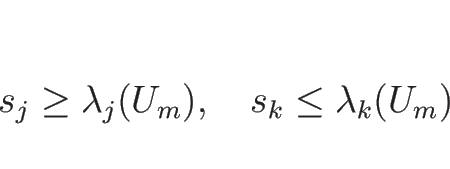
![]() をはさんで
をはさんで ![]() -膨張波と
-膨張波と ![]() -膨張波が並んでいる場合
(図 5.5) は、
-膨張波が並んでいる場合
(図 5.5) は、
![]() に接する波の端の部分を見れば
に接する波の端の部分を見れば
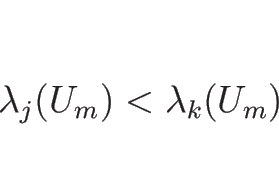
よって、いずれの場合も同じ始点を持つ 2 つの波が並ぶ場合は、
必ず ![]() が成り立つことがわかる。よって、
考えられる配置は、
左から 1,2,...,
が成り立つことがわかる。よって、
考えられる配置は、
左から 1,2,...,![]() という順の特性方向の波のみで、
その間に定数ベクトルが並ぶことになる。
という順の特性方向の波のみで、
その間に定数ベクトルが並ぶことになる。
竹野茂治@新潟工科大学