![\begin{displaymath}
U={\,}^T\!(u_1,u_2,\ldots,u_N)=\left[\begin{array}{c}u_1\\ u_2\\ \vdots\\ u_N\end{array}\right]
\end{displaymath}](img191.png)
![\begin{displaymath}
U={\,}^T\!(u_1,u_2,\ldots,u_N)=\left[\begin{array}{c}u_1\\ u_2\\ \vdots\\ u_N\end{array}\right]
\end{displaymath}](img191.png)
![\begin{displaymath}
F(U)={\,}^T\!(f_1(U),f_2(U),\ldots,f_N(U))
=\left[\begin{array}{c}f_1(U)\\ f_2(U)\\ \vdots\\ f_N(U)\end{array}\right]
\end{displaymath}](img195.png)
例えば、(2) で扱ったオイラー座標系の理想気体の
保存則方程式の場合は、
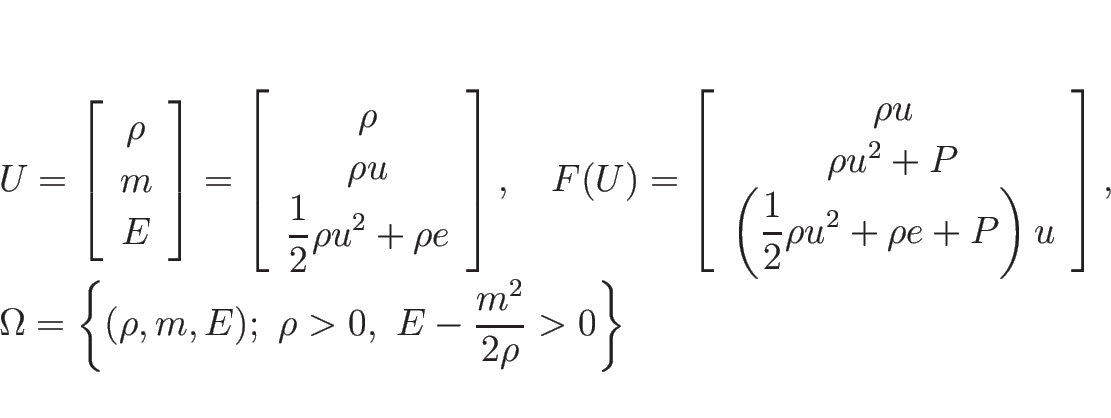
![]() の関数
の関数
![]() に対し、
に対し、![]() に関する微分演算子
に関する微分演算子
![]() を
を
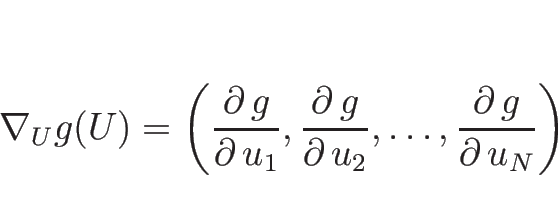
![\begin{displaymath}
\nabla_U F(U) = \left[\begin{array}{c}\nabla_U f_1(U)\\ \nab...
...e \frac{\partial\, f_N}{\partial\, u_N}\\
\end{array}\right]
\end{displaymath}](img203.png)
一般に、
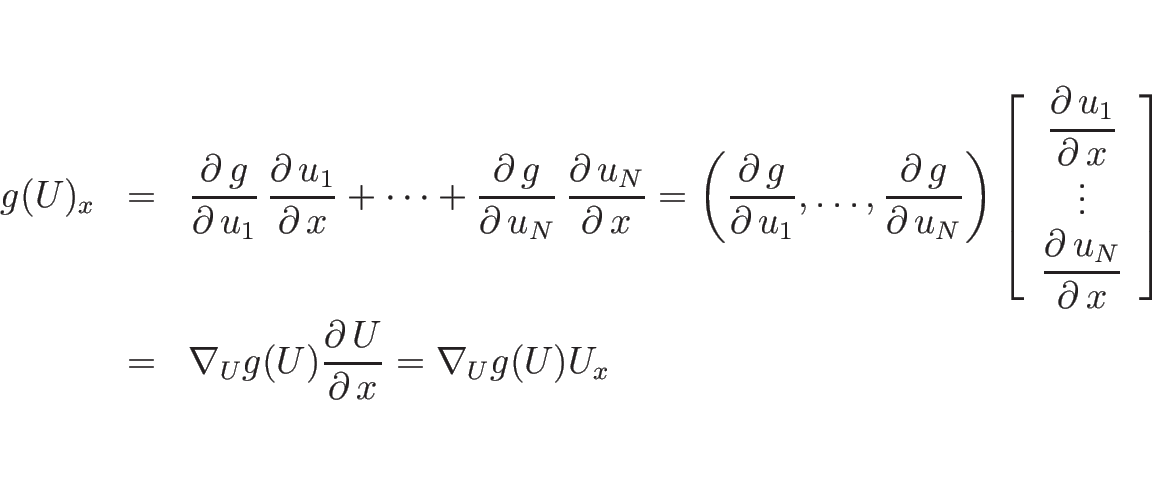
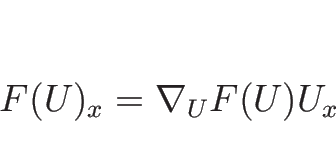
![]() に対して、
連立の準線形の 1 階の微分方程式 (3.3) の
係数行列
に対して、
連立の準線形の 1 階の微分方程式 (3.3) の
係数行列 ![]() の固有値がすべて異なる実数であるとき、
(3.3) は 双曲型 (hyperbolic)
であると呼ぶ。
その固有値を
の固有値がすべて異なる実数であるとき、
(3.3) は 双曲型 (hyperbolic)
であると呼ぶ。
その固有値を
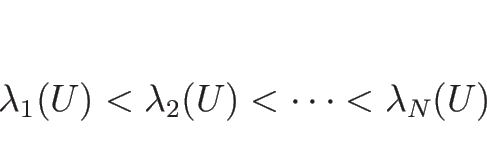
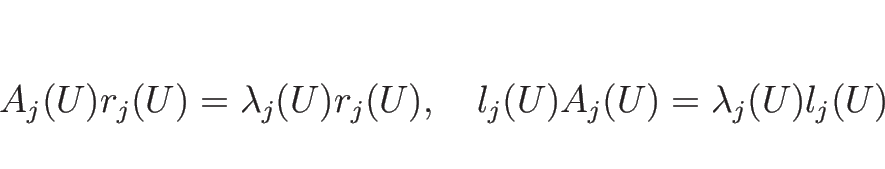
なお、![]() が
が ![]() で滑らかなときに、
で滑らかなときに、
![]() 全体で滑らかな
全体で滑らかな ![]() ,
, ![]() ,
, ![]() が
存在するかどうかについては、C.1 節を
参照のこと。
少なくとも局所的にはそれらが存在することは示せるので、
必要なら
が
存在するかどうかについては、C.1 節を
参照のこと。
少なくとも局所的にはそれらが存在することは示せるので、
必要なら ![]() を少し狭く考えることで、
を少し狭く考えることで、
![]() 上で滑らかな
上で滑らかな ![]() ,
, ![]() ,
, ![]() が
存在するとみなせる。
よって、以後はそのように考える (
が
存在するとみなせる。
よって、以後はそのように考える (![]() で存在する) こととする。
で存在する) こととする。