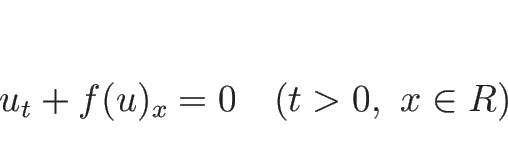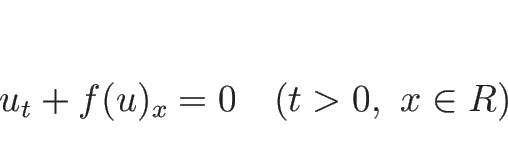3.1 はじめに
[1] では、単独の保存則方程式
(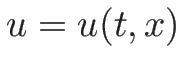 は未知、
は未知、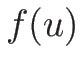 は
は 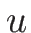 の関数として既知関数、
の関数として既知関数、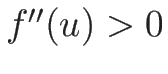 )
の、特に
)
の、特に 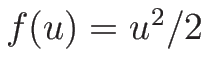 の Burgers 方程式の解について議論した。
そこに現われた膨張波、衝撃波のような解は、
本稿で扱う連立の保存則方程式 (保存則方程式系 と呼ぶ)
の Burgers 方程式の解について議論した。
そこに現われた膨張波、衝撃波のような解は、
本稿で扱う連立の保存則方程式 (保存則方程式系 と呼ぶ)
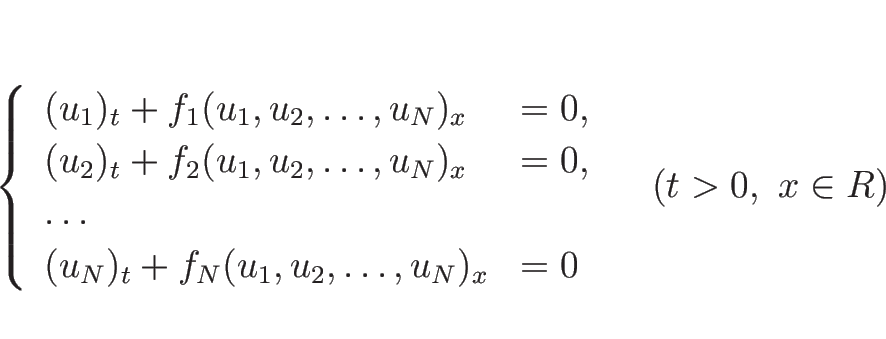 |
(3.20) |
(
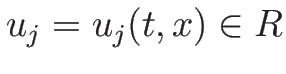 は未知、
は未知、
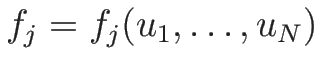 は
は
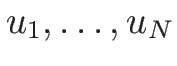 の既知関数
の既知関数
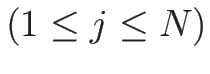 )
でも特徴的な解として表れ、一般的な解を構成する上でも重要な役割を果たす。
)
でも特徴的な解として表れ、一般的な解を構成する上でも重要な役割を果たす。
この節では、1 次元双曲型保存則方程式系に関する用語や、
リーマン問題の解を構成する要素の一つである膨張波について紹介する。
竹野茂治@新潟工科大学
2018-08-01