

Next: 4 Decay estimates
Up: Time-periodic solutions
Previous: 2 Preliminaries
(PDF file: paper9.pdf)
3 Approximate Solution
In this section, we construct an approximate solution of the
Lax-Friedrichs difference scheme type for the initial-boundary
value problem (1), (2)
in a standard way
(cf. [3],[4],[14].)
Let the initial data 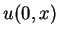 be a bounded measurable function and
be a bounded measurable function and
We suppose that the inverse of the 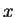 -mesh length
-mesh length 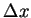 and
the ratio of the period
and
the ratio of the period 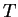 and the
and the 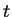 -mesh length are even
integers
-mesh length are even
integers 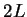 and
and 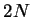 ,
,
It is necessary that the ratio of 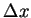 and
and 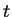 -mesh length
-mesh length
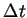 is a sufficiently large constant for the CFL condition.
We take the value such that
is a sufficiently large constant for the CFL condition.
We take the value such that
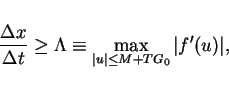 |
(17) |
where 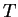 is time-period of function
is time-period of function 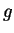 , and
, and 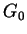 is the
maximum value of
is the
maximum value of 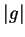
Let 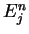 be an interval and
be an interval and 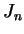 an index set such that
an index set such that
and we denote
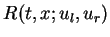 as the solution of the Riemann problem
(16).
as the solution of the Riemann problem
(16).
The approximation of the initial value
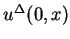 is defined as
a step value function
is defined as
a step value function
where 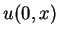 is extended to the function on
is extended to the function on
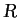 as the
as the 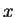 -periodic
function. The value
-periodic
function. The value 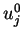 has the periodicity of
has the periodicity of
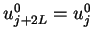 .
We define
.
We define
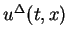 as the solution of the Riemann problem for the
step initial data
as the solution of the Riemann problem for the
step initial data
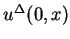
in each small regions
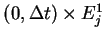 ,
, 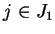 .
The wave must arrive at the top of the region by the CFL condition
(17).
On the line
.
The wave must arrive at the top of the region by the CFL condition
(17).
On the line 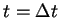 , we define
, we define
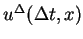 as the mean value
as the mean value
and construct
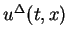 by solutions of Riemann problems
in
by solutions of Riemann problems
in
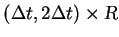 similarly in
similarly in
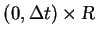 ,
,
On 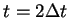 , we set
, we set
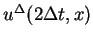 as the sum of the mean value and
the term for the outer force
as the sum of the mean value and
the term for the outer force
The last calculation is called the fractional step method.
For
![$(2n\Delta t,(2n+2)\Delta t]\times {\mbox{\sl R}}$](img102.gif) (
(
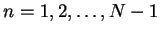 ) we define the
approximation
) we define the
approximation
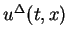 by the similar way.
The following lemma shows that above construction can be
continued to
by the similar way.
The following lemma shows that above construction can be
continued to 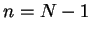 .
.
LEMMA 2
If constants
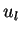
and
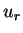
satisfy
then the solution of the Riemann problem (
16)
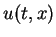
satisfies
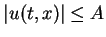
.
By Lemma 2, it is easy to show that
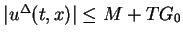 and waves appeared in the definition
of
and waves appeared in the definition
of
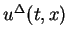 cannot access in
cannot access in
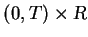 from the CFL
condition (17) because speeds of
these waves do not over the maximum value of
from the CFL
condition (17) because speeds of
these waves do not over the maximum value of 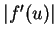 .
.

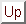

Next: 4 Decay estimates
Up: Time-periodic solutions
Previous: 2 Preliminaries
Shigeharu TAKENO
15 January 2002
![]() be a bounded measurable function and
be a bounded measurable function and
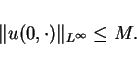
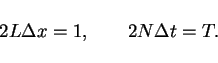
![\begin{displaymath}
G_0 = \max_{[0,T]\times[0,1]}\vert g(t,x)\vert.
\end{displaymath}](img80.gif)
![]() be an interval and
be an interval and ![]() an index set such that
an index set such that
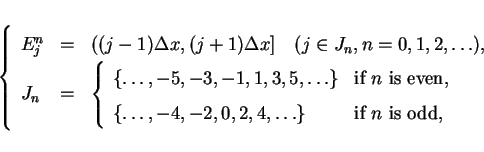
![]() is defined as
a step value function
is defined as
a step value function
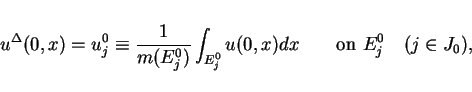
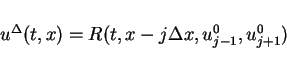
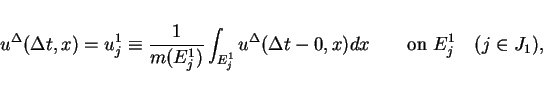
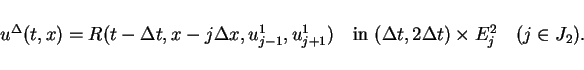
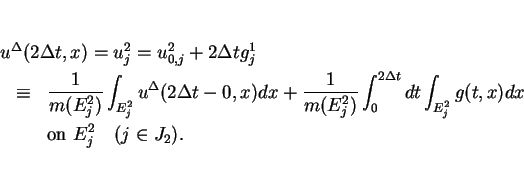
![]() (
(
![]() ) we define the
approximation
) we define the
approximation
![]() by the similar way.
The following lemma shows that above construction can be
continued to
by the similar way.
The following lemma shows that above construction can be
continued to ![]() .
.
![]() and waves appeared in the definition
of
and waves appeared in the definition
of
![]() cannot access in
cannot access in
![]() from the CFL
condition (17) because speeds of
these waves do not over the maximum value of
from the CFL
condition (17) because speeds of
these waves do not over the maximum value of ![]() .
.