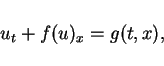(PDF file: paper9.pdf)

1 Introduction

In this paper we study a scalar conservation law with an outer force term

$$u_t+f(u)_x = g(t,x),$$ (1)

where the function $f(u)$ is smooth and convex. The global existence of weak solutions of the Cauchy problem (1) for any large initial data was proved in [11]. If initial data $u_0(x)$ and an outer force $g(t,x)$ are $x$-periodic functions then the solution $u(t,x)$ may be periodic and may be regarded as a solution of the initial-boundary value problem (1) and

$$\left\{\begin{array}{ll} u(0,x)=u_0(x) & (0<x<1),\\ u(t,0)=u(t,1) & (t>0). \end{array}\right.$$ (2)

We consider the following problem:

If $g(t,x)$ is a time-periodic function with period $T$, does a time-periodic solution exist with the same period, assuming the necessary condition

$$\int_0^T dt \int_0^1 g(t,x)dx=0$$ (3)

for the outer force term $g(t,x)$ ?

For the existence of a time periodic solution, we need the decay of the solution to the homogeneous equation

$$u_t+f(u)_x=0,$$ (4)

with data (2). The decay to the mean value

$$\bar{u} = \int_0^1 u(t,x)dx = \int_0^1 u_0(x)dx$$

was obtained under some regularity assumption for the solution at a (slow) rate $1/t$ in [7].

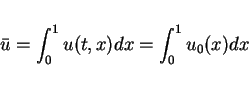
For the viscous equation

$$\left\{\begin{array}{l} u_t+f(u)_x = \varepsilon u_{xx} \h... ...1em}u_x(t,0)=u_x(t,1) \hspace{2em}(t>0),\\ \end{array}\right.$$ (5)

and the homogeneous equation with positive linear term

$$\left\{\begin{array}{l} u_t+f(u)_x + \varepsilon u = 0 \hs... ...1),\\ u(t,0)=u(t,1) \hspace{2em}(t>0),\\ \end{array}\right.$$ (6)

solutions decay at a faster rate assuming $\varepsilon$ is a positive constant. The fast decay for each equation gives a sharp enough estimate to demonstrate the existence of a fixed point of the Poincare map $u(0,x)\mapsto u(T,x)$ for each equation with the time-periodic outer force $g(t,x)$. For systems of conservation laws, Matsumura-Nishida ([9]) proved the existence of periodic solutions for viscous isothermal gas equations for any large periodic outer force, and Matsumura-Yanagi ([10]), Yanagi ([16]) extended the results to the case of viscous isentropic gases. Feireisl ([6]) proved the existence of periodic solutions for systems of hyperbolic conservation laws with positive linear term. For such systems, solutions of the approximation for the homogeneous systems decay fast uniformly, and he made the sequence of the periodic solutions for the viscous approximation and showed the convergence by using the compensated compactness theory.

However, even in the scalar case, we cannot obtain the time-periodic solution of our problem as the limit of the periodic solutions of equation added $g(t,x)$ to (5) and (6) as $\varepsilon \rightarrow 0$. This is because the estimates for fast decay depend on the constant $\varepsilon$ and are not valid in the limit $\varepsilon \rightarrow 0$, and, according to [7], it does not imply that the decay is fast for the limit equation (4).

On the other hand, the standard method for the proof of the existence of the weak solution to the equation (1) is to show the convergence of some approximate solutions which are constructed by a difference scheme method or the artificial viscosity method (5).

Tadmor ([13]) proved the slow decay for the Lax-Friedrichs difference approximations, which does not depend on the mesh size. Note that this is obtained from Oleinik's entropy condition ([11]) and from the periodicity of the boundary condition. We can to solve our problem by such a uniform estimate.

We remark that any such uniform estimates have not been obtained for the approximations of systems of conservation laws for large initial data, and therefore the existence of periodic solutions for systems of equations is still open.

Our result is the following.

THEOREM 1   Under assumptions (14) and (15) for $f$ and $g$, the problem (1), (7) has a time periodic weak solution $u(t,x)$ for any average $\bar{u}$, and the solution satisfies the entropy condition (13).

We remark that the periodic solution of the problem (1), (7) is not unique with respect to $g$ and $\bar{u}$.

The outline of the proof of Theorem 1 is the followings. We construct a Lax-Friedrichs difference approximation for the problem (1), (7) and we will obtain the estimate of uniform bounds for it by the methods similar to those of Tadmor ([13]) in §4. The Poincare map is regarded as on the finite dimensional space for the difference approximation because the approximate solution has values at each finite point for fixed $t$. We show the map takes a closed convex set into the same set. Hence we can use Brouwer's fixed point theorem for the existence of the fixed point of the map from the continuity of the approximation. Since these fixed points are uniformly bounded with respect to the any mesh lengths, we obtain a subsequence that converges to a weak solution by the compensated compactness theory ([15]). We check the compactness of the entropy for the approximation in §5 for the last convergence, and show the limit is a weak solution of the problem (1), (7) satisfying the entropy condition in §6.