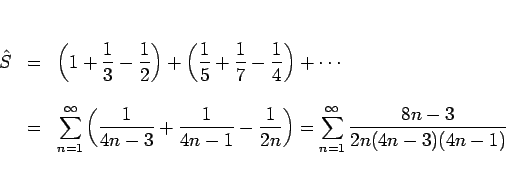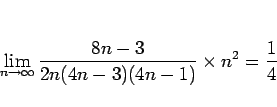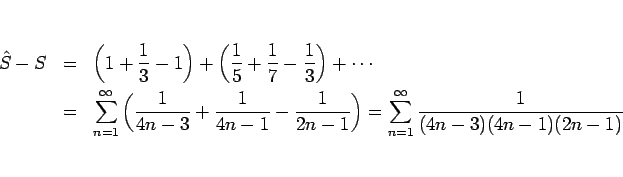単調増加数列 ![]() は、上に有界ならばある値に収束する。
上に有界でなければ
は、上に有界ならばある値に収束する。
上に有界でなければ ![]() に発散する。
に発散する。
これは、実数の定義と深く関わる定理で、証明は省略する。
なお、数列 ![]() が 上に有界である とは、
が 上に有界である とは、
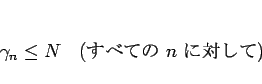
よって正項級数は、上に有界で収束するか、
![]() に発散するか、のいずれかとなる。
に発散するか、のいずれかとなる。
この定理 4 から、 次のこともすぐにわかる。
![]() のとき、
のとき、
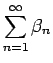 が収束するならば
が収束するならば
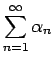 も収束する
も収束する
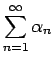 が発散するならば
が発散するならば
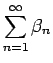 も発散する
も発散する
この命題は、以下のようにもう少し拡張することもできる。
![]() ,
, ![]() で、
で、
![]() のとき、
のとき、
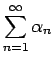 の収束、発散と
の収束、発散と
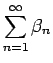 の収束、発散とは一致する。
の収束、発散とは一致する。
証明
![]() より、
十分大きい
より、
十分大きい ![]() より先の
より先の ![]() に対しては
少なくとも
に対しては
少なくとも
![]() が成り立つ2。
よって、
が成り立つ2。
よって、![]() に対しては、
に対しては、
![]() , および
, および
![]() となるから、
命題 5 より
となるから、
命題 5 より
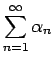 の収束、発散と
の収束、発散と
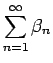 の収束、発散とは一致する
(収束、発散は、十分先の
の収束、発散とは一致する
(収束、発散は、十分先の ![]() のみで考えればよい)。
のみで考えればよい)。
無限級数 (1) が 絶対収束する とは、
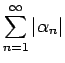 が有限の値に収束することを言う
3。
が有限の値に収束することを言う
3。
絶対収束する無限級数は収束する。
証明
実数 ![]() に対して、正の部分
に対して、正の部分 ![]() と負の部分
と負の部分 ![]() を次のように
定める:
を次のように
定める:
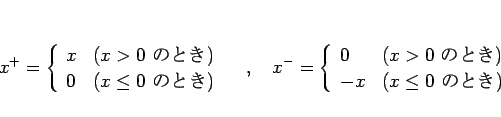
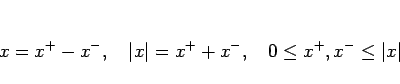
これを用いて、
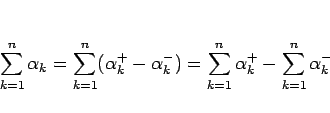
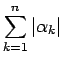 は有限の値に収束するから、
命題 5 より
は有限の値に収束するから、
命題 5 より
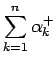 ,
,
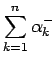 も有限の値に収束する。
よって、
も有限の値に収束する。
よって、
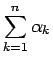 も有限の値に収束する。
も有限の値に収束する。
(1) が絶対収束するとき、
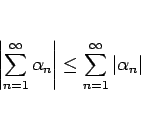
証明
上の命題 7 の証明から
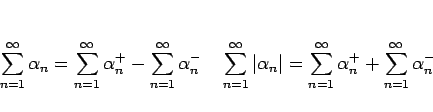
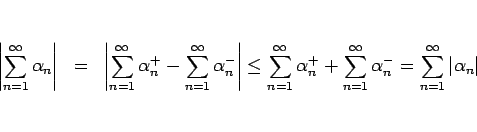
しかし、命題 7 の逆は言えない。つまり、
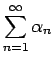 は収束しても
は収束しても
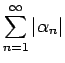 が収束するとは限らない。
例えば、
が収束するとは限らない。
例えば、
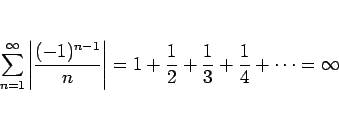
このように、収束はするが絶対収束しない級数を、条件収束 するという。 一般に条件収束級数の取り扱いは厄介であり、 級数に関する性質の多くは絶対収束級数に対するものである。 ここでは条件収束級数の厄介さを物語る次の命題のみを証明なしに紹介しておく。
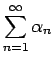 に対しては、
に対しては、
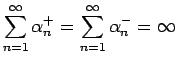 、
すなわち、正の部分も負の部分も無限大に発散する。
、
すなわち、正の部分も負の部分も無限大に発散する。
ここでいう「無限回の項の順序の入れ変え」とは
単に級数の 3 番目と 4 番目の項だけを入れかえる、
ということではなく (それでは値は変わらない)、
例えば (4) で言えば、
負の項が 2 つおきになるように後ろにずらして、
![]() は、命題 3 より 2 つずまとめて考えると、
は、命題 3 より 2 つずまとめて考えると、
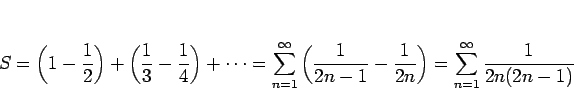
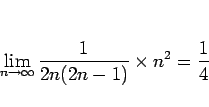
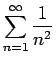 は収束するから、
命題 6 より
は収束するから、
命題 6 より
一方 ![]() は、命題 3 より 3 つずまとめると
は、命題 3 より 3 つずまとめると