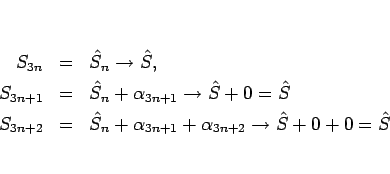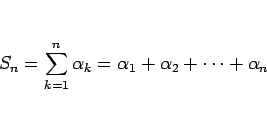 |
(2) |
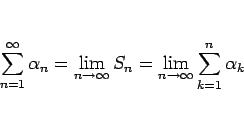
収束しない場合、発散する という。例えば、
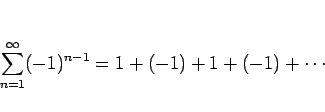

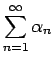 が収束するならば
が収束するならば
![]()
証明
![]() (
(![]() ) なので、
仮定より
) なので、
仮定より
![]() のとき
のとき
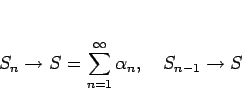
この命題 1 の逆、すなわち
![]() であったとしても
であったとしても
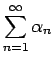 が収束するとは限らない。
例えば、
が収束するとは限らない。
例えば、
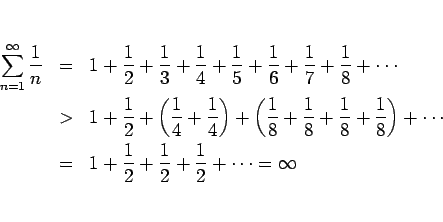
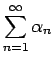 が発散することは言える。
が発散することは言える。
収束級数に対しては、容易に次も言える (証明は省略)。
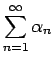 ,
,
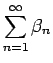 が収束する級数であるとき、
が収束する級数であるとき、
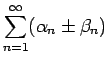 も収束し、
も収束し、
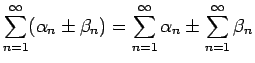
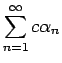 も収束し、
も収束し、
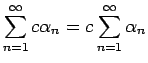
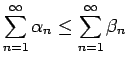
また級数は、いくつかの項をまとめて考えても 収束、発散は変わらないことが言える。
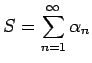 に対して、
に対して、
![]() を
を ![]() 個ずつまとめた項からなる数列
個ずつまとめた項からなる数列 ![]() を
を
![\begin{eqnarray*}\beta_1 &=& a_1+a_2+\cdots+a_m\\
\beta_2 &=& a_{m+1}+a_{m+2}+...
...cdots+a_{3m}\\
\lefteqn{\makebox[0.3\linewidth][l]{\dotfill}}
\end{eqnarray*}](img32.gif)
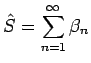 とすると、
とすると、
証明
簡単のため、![]() として証明する。
として証明する。
![]() ,
, ![]() の部分和をそれぞれ
の部分和をそれぞれ ![]() ,
, ![]() と
書くことにすると、
と
書くことにすると、
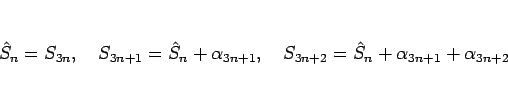
逆に、
![]() のとき、
のとき、