3 地球のような星の場合
地球のような星の場合、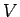 は球で1、
さらに、その質量は中心から層状に対称に分布すると考えられるので、
地球の中心を原点 O とすれば、
は球で1、
さらに、その質量は中心から層状に対称に分布すると考えられるので、
地球の中心を原点 O とすれば、
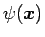 は
は
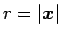 のみの関数
のみの関数
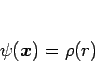
と見ることができる2。
この条件の元で (1) を
極座標変換を用いて計算してみる。
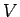 は半径
は半径 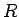 の球であるとし、極座標を
の球であるとし、極座標を
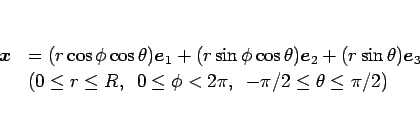 |
(2) |
のように導入する。
ここで、
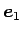 ,
,
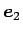 ,
,
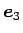 は
互いに直交する単位ベクトルとするが、
軸方向の基本ベクトルと取る必要はないので、
計算を簡単にするため、
は
互いに直交する単位ベクトルとするが、
軸方向の基本ベクトルと取る必要はないので、
計算を簡単にするため、
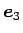 を
を
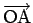 の方向に取り、
の方向に取り、
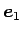 ,
,
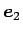 はそれに応じて取り直すこととする。
ただし、A = O の場合は後で別に考えることとし、
まずは
はそれに応じて取り直すこととする。
ただし、A = O の場合は後で別に考えることとし、
まずは
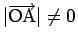 の場合を考える。
この場合は、
の場合を考える。
この場合は、
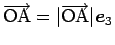 となることに注意する。
となることに注意する。
まずはこの変数変換のヤコビアン
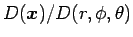 であるが、
これは
であるが、
これは
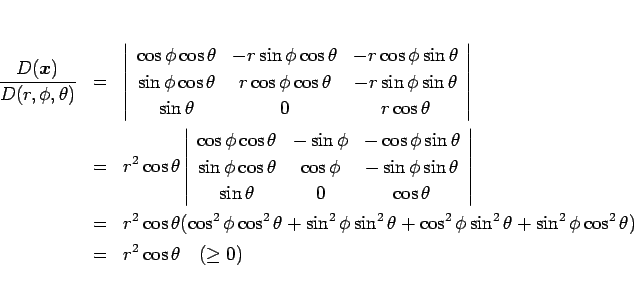
となる。また、
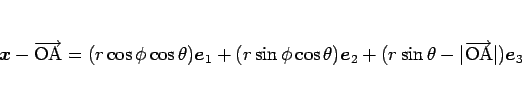
より、
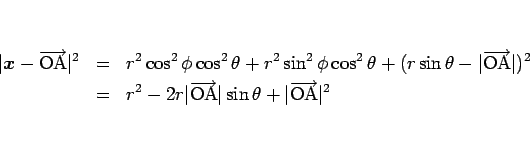
となるので、(1) は極座標 (2) により
以下のようになる:
ここで、
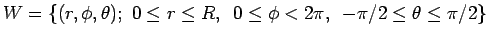 であり、
であり、
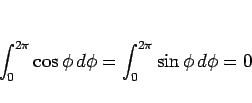
なので、
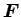 の
の
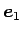 ,
,
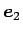 方向成分は 0 となり、
よって
方向成分は 0 となり、
よって
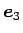 成分のみ残ることになるが、
これは
成分のみ残ることになるが、
これは 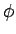 にはよらないので、
にはよらないので、
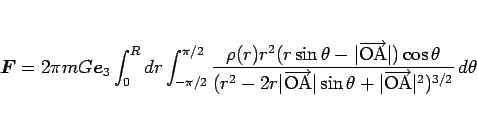 |
(4) |
となる。
今、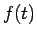 (
(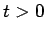 ) を、
) を、
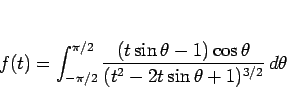 |
(5) |
とすると、
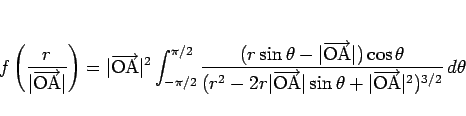
なので、(4) は 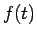 を用いて
を用いて
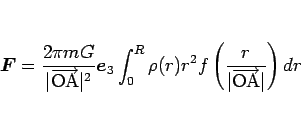 |
(6) |
と書けることになる。
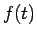 を積分するために
を積分するために
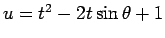 と置換すると、
と置換すると、
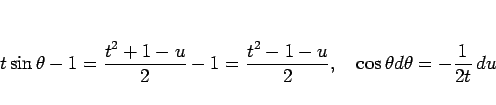
より、 のとき
のとき 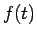 は
は
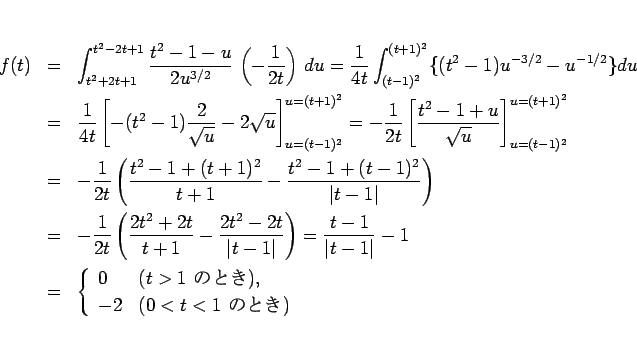
と計算される。よって、これを (6) に代入すると、結局
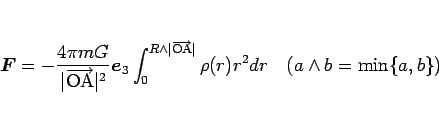 |
(7) |
と書けることになる。
さらに、地球の中心から半径 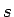 (
(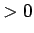 ) までの部分の球の質量を
) までの部分の球の質量を 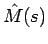 と書くことにすると、
と書くことにすると、
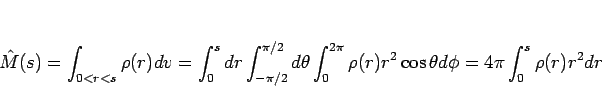
となるので、これを用いれば (7) は、
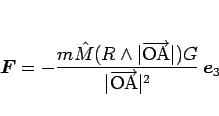 |
(8) |
と書くこともできる。
なお、A=O の場合は
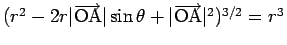 となるので、
(3) は、
となるので、
(3) は、
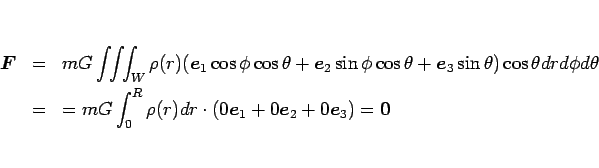
となる。
しかも、この計算は、
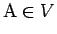 の場合の広義積分が
発散せずに収束することも示していることに注意する。
の場合の広義積分が
発散せずに収束することも示していることに注意する。
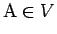 の場合、A を中心とする小さな球 (A の近傍) の積分は、
A を中心とする極座標で積分すれば、
の場合、A を中心とする小さな球 (A の近傍) の積分は、
A を中心とする極座標で積分すれば、
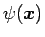 が
が 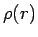 ではなく
ではなく 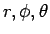 に依存する関数となるので
に依存する関数となるので
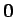 にはならないが、
それ以外は上の計算とほぼ同じで分母の
にはならないが、
それ以外は上の計算とほぼ同じで分母の 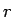 は分子の
は分子の 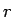 と
丁度約分されてしまうので、積分は発散せずに収束することがわかる。
と
丁度約分されてしまうので、積分は発散せずに収束することがわかる。
竹野茂治@新潟工科大学
2013年1月6日
![]() は半径
は半径 ![]() の球であるとし、極座標を
の球であるとし、極座標を
![]() であるが、
これは
であるが、
これは
![]() を積分するために
を積分するために
![]() と置換すると、
と置換すると、
![]() (
(![]() ) までの部分の球の質量を
) までの部分の球の質量を ![]() と書くことにすると、
と書くことにすると、
![]() となるので、
(3) は、
となるので、
(3) は、