4 等時降下曲線の解
式 (5) の被積分関数も、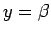 で分母が 0 になるので、
(5) を単純に
で分母が 0 になるので、
(5) を単純に 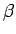 で微分することはできないが、
実は良く知られているように、(5) の左辺は
で微分することはできないが、
実は良く知られているように、(5) の左辺は 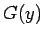 の 1/2 階積分 (の定数倍) の形なので、
この式をもう 1/2 階積分すれば
の 1/2 階積分 (の定数倍) の形なので、
この式をもう 1/2 階積分すれば 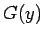 については
簡単な式になることが期待される。
については
簡単な式になることが期待される。
すなわち、両辺を
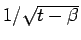 倍して、
倍して、
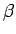 に関して 0 から
に関して 0 から 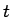 まで積分する (
まで積分する (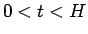 )。
)。
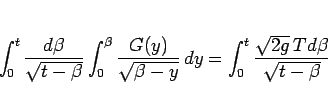 |
(6) |
(6) の左辺の累次積分は、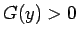 より順序交換でき、
より順序交換でき、
となる。ここで、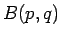 はベータ関数で、良く知られているように
はベータ関数で、良く知られているように
である。一方 (6) の右辺は、
なので、結局
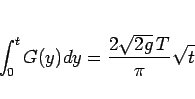 |
(7) |
が、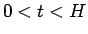 である任意の
である任意の 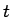 に対して成り立つことになる。
この式を
に対して成り立つことになる。
この式を 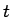 で微分すれば、
で微分すれば、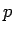 に対する方程式
に対する方程式
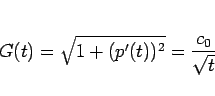 |
(8) |
が得られる (
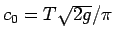 )。
)。
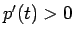 より、(8) から
より、(8) から
となるので、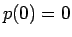 より結局
より結局
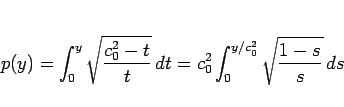 |
(9) |
となる。
あとはこの積分を求めればよい。積分
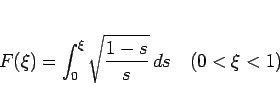 |
(10) |
は、置換
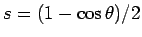 , (
, (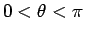 ) により、
) により、
となる。
ここで、
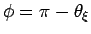 とすると、
とすると、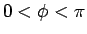 で、
で、
となり、これは [1] で見たように、
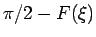 が
が 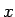 軸、
軸、
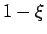 が
が 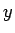 軸のサイクロイド (の 1/2 縮小版) の左半分を表すので、
軸のサイクロイド (の 1/2 縮小版) の左半分を表すので、
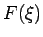 は、それを
は、それを 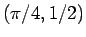 を中心に上下、左右に反転したもの (
を中心に上下、左右に反転したもの (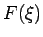 が
が 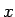 軸、
軸、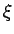 が
が 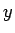 軸)、
すなわち「逆さサイクロイド」の右半分のグラフになり、
原点がその最下点となる (図 2)。
軸)、
すなわち「逆さサイクロイド」の右半分のグラフになり、
原点がその最下点となる (図 2)。
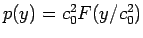 なので、
なので、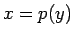 は
それを
は
それを 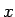 ,
, 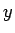 方向に
方向に 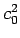 倍したものであり、
やはり逆さサイクロイドが解となることがわかる。
倍したものであり、
やはり逆さサイクロイドが解となることがわかる。
竹野茂治@新潟工科大学
2017年3月22日
![]() 倍して、
倍して、
![]() に関して 0 から
に関して 0 から ![]() まで積分する (
まで積分する (![]() )。
)。
![]() なので、
なので、![]() は
それを
は
それを ![]() ,
, ![]() 方向に
方向に ![]() 倍したものであり、
やはり逆さサイクロイドが解となることがわかる。
倍したものであり、
やはり逆さサイクロイドが解となることがわかる。