3 誤差関数の漸近展開
漸近展開の対象となる関数は、それなりに厄介な関数である場合が多く、
またテイラー展開のように決まった方法もあまりないので、
個別に特別な方法で求めていくことが多いようである。
本節ではまずそのような例の 1 つとして誤差関数
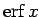 の漸近展開を
考えてみることにする。
の漸近展開を
考えてみることにする。
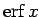 は、次の式で定義される関数である。
は、次の式で定義される関数である。
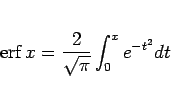
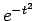 の不定積分を簡単な関数で表すことはできないので、
の不定積分を簡単な関数で表すことはできないので、
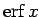 を積分を使わずに書くことはできない。
を積分を使わずに書くことはできない。
しかし、
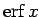 は微分が
は微分が
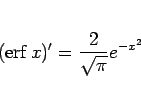
と簡単な式で書けるので、
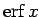 の場合はロピタルの定理を用いて
漸近展開を得ることができる。
の場合はロピタルの定理を用いて
漸近展開を得ることができる。
よく知られているように、
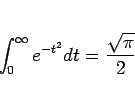
であるから、
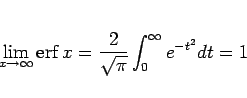
となる。これは、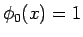 が第 1 近似であることを示している。
第 2 近似は
が第 1 近似であることを示している。
第 2 近似は
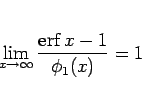 |
(4) |
となる  を見つければよいのであるが、
(4) の分子を荒く評価すると、
を見つければよいのであるが、
(4) の分子を荒く評価すると、
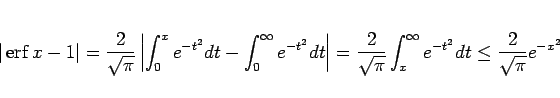
であるから、
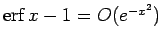 であることがわかる。
よって
であることがわかる。
よって
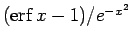 の極限を考えてみると、
これは
の極限を考えてみると、
これは 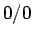 の不定形なので、ロピタルの定理により、
の不定形なので、ロピタルの定理により、
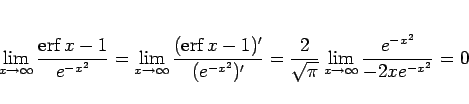
となってしまうので、実際には
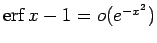 であり、
この分母では少し大きい。よって、
であり、
この分母では少し大きい。よって、
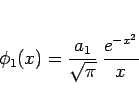
としてみると、
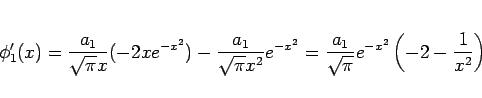
であるから、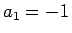 とすれば (4) が成り立つことが
ロピタルの定理によりわかる。
すなわち第 2 近似は、
とすれば (4) が成り立つことが
ロピタルの定理によりわかる。
すなわち第 2 近似は、
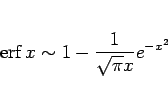 |
(5) |
となる。同様に第 3 近似は
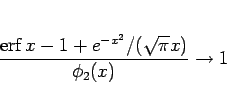 |
(6) |
となる 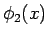 を見つければよいが、
を見つければよいが、
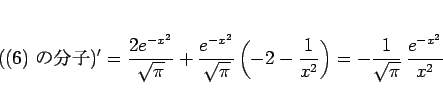
なので
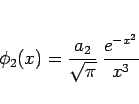
とすれば
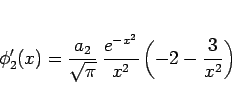
となるから 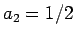 とすればよい。よって第 3 近似は、
とすればよい。よって第 3 近似は、
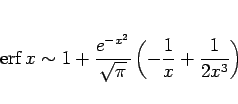
となる。以下、同様に第 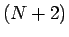 近似は
近似は
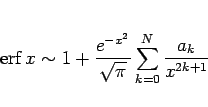
の形となる。この 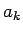 を求める。この場合は、
を求める。この場合は、
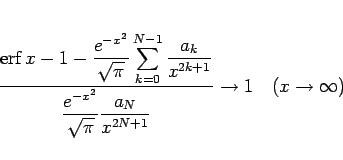 |
(7) |
となるわけであるが、
であるから、(7) が成り立つには、
(8) のかっこ内の 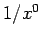 から
から 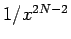 までの
項がすべて消える必要がある。よって、
までの
項がすべて消える必要がある。よって、
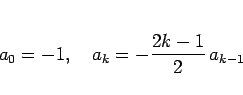
が成り立つ必要があり、ここから
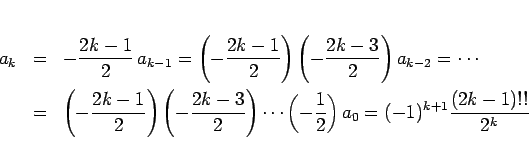
となることがわかる。ここで、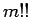 は、
は、
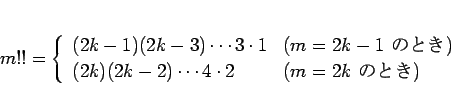
を表す記号で、さらに 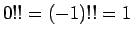 であるとする。
なお、この
であるとする。
なお、この 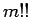 は、以下のように通常の階乗を用いて表すこともできる。
は、以下のように通常の階乗を用いて表すこともできる。
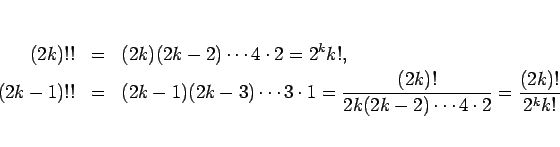
結局、
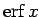 の漸近展開は
の漸近展開は
となることがわかった。
なお、(9) の右辺は無限和の形で書いているが、
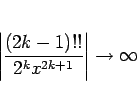 |
(10) |
であるから、この級数は無限級数としては発散級数であり、
よってこの右辺はあくまで定義 1 の意味での和であることに注意する。
この (10) が成り立つことは、
次の項との絶対値の比を考えればわかる。
その比は
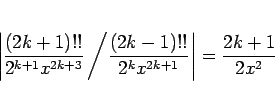
であるが、これはどのような 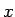 に対しても、
あるところからは 1 を越えて大きくなる。
(10) の左辺はそのような数を
順にかけて作られる数列であるから、
よって (10) が成り立つことになる。
に対しても、
あるところからは 1 を越えて大きくなる。
(10) の左辺はそのような数を
順にかけて作られる数列であるから、
よって (10) が成り立つことになる。
竹野茂治@新潟工科大学
2010年4月8日
![]() は、次の式で定義される関数である。
は、次の式で定義される関数である。
![]() は微分が
は微分が
![]() の漸近展開は
の漸近展開は