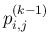
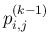
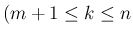 ) を
具体的な式で書き表す。
なお、分母の
) を
具体的な式で書き表す。
なお、分母の
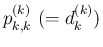 が 0 ではないという
保証もないので、それも同時に考える。
が 0 ではないという
保証もないので、それも同時に考える。
まずは 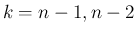 の場合を考える。
(35) で
の場合を考える。
(35) で 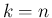 とすると、
(32) より
とすると、
(32) より 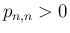 で、
で、
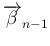 と
と
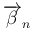 は
は 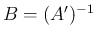 の
列ベクトルだから線形独立で、よって補題 6 より
の
列ベクトルだから線形独立で、よって補題 6 より
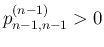 であることが保証される。
であることが保証される。
そして、これに対し (35) で 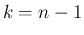 とすると、
とすると、
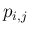 で表す。
(48) の行列式の 4 つの成分は、
(46) より、
で表す。
(48) の行列式の 4 つの成分は、
(46) より、
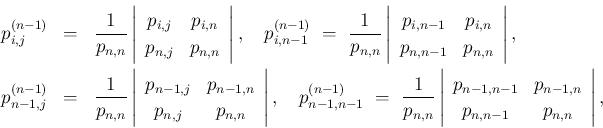
![\begin{eqnarray*}p^{(n-1)}_{i,j} &=& \frac{1}{p_{n,n}}\left\vert X^{[2]}_{[2]}\r...
...-1,n-1} \ =\ \frac{1}{p_{n,n}}\left\vert X^{[1]}_{[1]}\right\vert\end{eqnarray*}](img331.png)
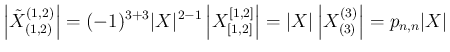
次は、
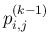 の一般項を求める。
まず、
の一般項を求める。
まず、
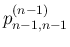 は (47) より
は (47) より
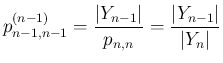
 は (51) より
は (51) より
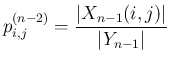
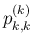 (
(
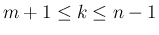 )、
および
)、
および
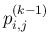 (
(
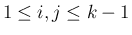 ) を
と予想し、これを帰納法で証明する。
なお、すべての
) を
と予想し、これを帰納法で証明する。
なお、すべての 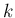 に対し
に対し 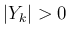 であることは、
補題 6 により保証されるので、
(55) が成り立てば、
であることは、
補題 6 により保証されるので、
(55) が成り立てば、
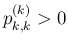 も言えることになる。
も言えることになる。
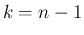 に対しては上で示した通り成立する。
なお、
に対しては上で示した通り成立する。
なお、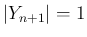 と考えれば、
と考えれば、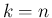 に対しても
(46) より
に対しても
(46) より
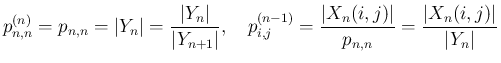
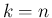 でも成立することになる。
でも成立することになる。
以下、
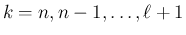 までは成立したとして、
までは成立したとして、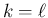 の場合に
成立することを示す (
の場合に
成立することを示す (
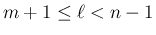 )。
)。
(55) の後者の 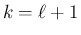 の式より、
の式より、
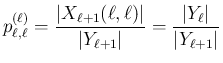
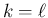 の最初の式が得られる。
後は (55) の後者の
の最初の式が得られる。
後は (55) の後者の 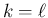 の式を示せばよい。
漸化式 (35) より、
の式を示せばよい。
漸化式 (35) より、
![$\displaystyle p^{(\ell-1)}_{i,j}
= \frac{1}{p^{(\ell)}_{\ell,\ell}}
\left\vert...
...ll}\\ [.5zh]
p^{(\ell)}_{\ell,j}&p^{(\ell)}_{\ell,\ell}\end{array}\right\vert
$](img359.png)
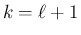 の式より、
の式より、
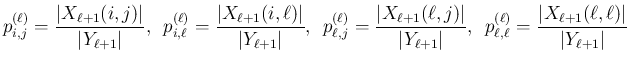
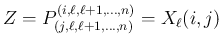
![$\displaystyle p^{(\ell)}_{i,j}=\frac{\left\vert Z^{[2]}_{[2]}\right\vert}{\vert...
..._{\ell,\ell}=\frac{\left\vert Z^{[1]}_{[1]}\right\vert}{\vert Y_{\ell+1}\vert}
$](img362.png)
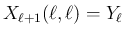 より、
より、
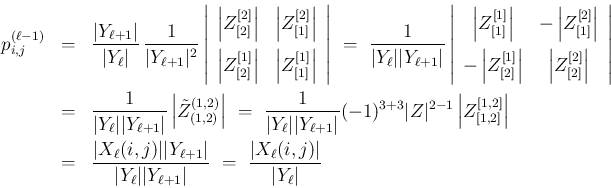
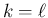 の
式も得られた。
これで、帰納法により確かに (55) が
成立することが証明された。
の
式も得られた。
これで、帰納法により確かに (55) が
成立することが証明された。
よって、(55) で 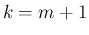 とすれば、
最終的な係数
とすれば、
最終的な係数
竹野茂治@新潟工科大学