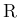
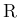 上の積分なので、
その積分は、(29) の
上の積分なので、
その積分は、(29) の
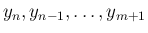 に関する平方完成の計算に帰着される。
それを計算するために、係数、特に
に関する平方完成の計算に帰着される。
それを計算するために、係数、特に
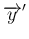 の 2 次の項の係数に
対する漸化式を作る。
の 2 次の項の係数に
対する漸化式を作る。
まず、(29) を 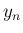 に関して平方完成してみる。
に関して平方完成してみる。
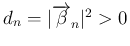 であることに注意する。
(29) の右辺を
であることに注意する。
(29) の右辺を
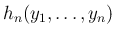 と
書くことにすると、そこに含まれる
と
書くことにすると、そこに含まれる 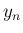 に関する項は
に関する項は
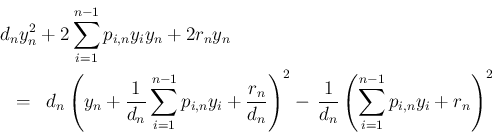
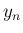 での積分後に残って、
での積分後に残って、
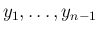 の項として追加されることになる。
よって、
の項として追加されることになる。
よって、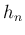 のうち
のうち 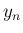 の平方部分を除いたものを
の平方部分を除いたものを
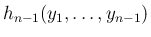 とすると、
とすると、
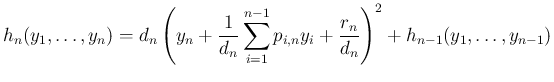
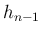 は、
は、
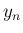 での積分は
での積分は 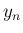 の平方完成部分の積分が
の平方完成部分の積分が
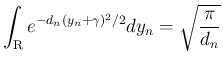
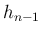 だけが残る。
次は
だけが残る。
次は 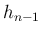 を
を 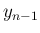 に関して平方完成を行う、という
計算になる。
この平方完成部分以外の項
に関して平方完成を行う、という
計算になる。
この平方完成部分以外の項
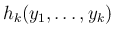 の係数に関する
漸化式を作る。
とすると (
の係数に関する
漸化式を作る。
とすると (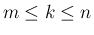 )、
)、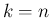 に対しては、
で、
に対しては、
で、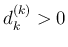 であれば上の計算と同様に、
となり (
であれば上の計算と同様に、
となり (
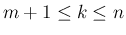 )、
)、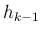 の係数は、
(30) と同様に、
の係数は、
(30) と同様に、
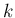 に関して逆向きの) 漸化式となる。
なお、
と定義すると、
に関して逆向きの) 漸化式となる。
なお、
と定義すると、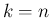 に対しては自然に
に対しては自然に
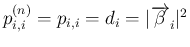 、
、
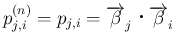 となり、
となり、
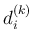 に関する漸化式 (34) は
に関する漸化式 (34) は
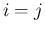 に対する (35) に含まれることになるから、
(35) は、
と書くことができる。以降主にこの漸化式を考えることにする。
に対する (35) に含まれることになるから、
(35) は、
と書くことができる。以降主にこの漸化式を考えることにする。
竹野茂治@新潟工科大学