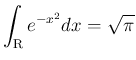 (8)
(8)
証明
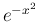 は偶関数なので、
は偶関数なので、
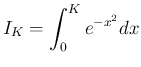
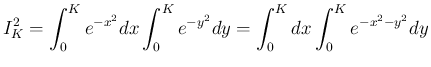
![$D_K=[0,K]\times[0,K]$](img48.png) 上の二重積分と見ることができる。
上の二重積分と見ることができる。
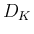 は、原点中心半径
は、原点中心半径 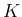 の 1/4 円
の 1/4 円 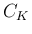 を含み、
原点中心半径
を含み、
原点中心半径 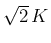 の 1/4 円
の 1/4 円
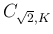 に含まれるので、
となる。ここで、
に含まれるので、
となる。ここで、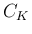 の積分を極座標変換すれば、
の積分を極座標変換すれば、
![$\displaystyle \int\!\!\int _{C_K}e^{-x^2-y^2}dxdy
= \int_0^{\pi/2}d\theta\int_...
...}\left[-\,\frac{1}{2}e^{-r^2}\right]_{r=0}^{r=K}
= \frac{\pi}{4}(1-e^{-K^2})
$](img55.png)
![[*]](crossref.png) ) より、
となる。ここで
) より、
となる。ここで
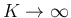 とすれば、
はさみうちの原理により、
とすれば、
はさみうちの原理により、
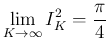
![[*]](crossref.png) ) が得られる。
) が得られる。
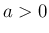 ,
, 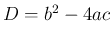 に対して、
に対して、
証明
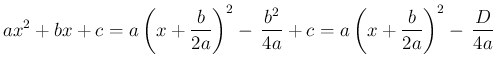
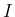 とすると、
とすると、
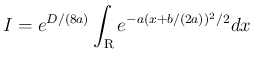
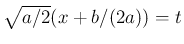 と置換すれば、
補題
と置換すれば、
補題 ![[*]](crossref.png) より
より
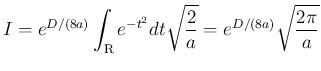
竹野茂治@新潟工科大学