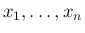 が独立で、
が独立で、
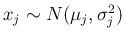 (
(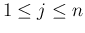 ) であるとき、定数
) であるとき、定数 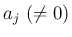 ,
, 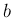 に対し、
に対し、
確率変数
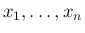 が独立で、
が独立で、
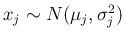 (
(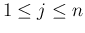 ) であるとき、定数
) であるとき、定数 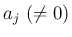 ,
, 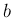 に対し、
に対し、
これをいくつかの段階に分けて考える。
確率変数
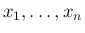 が独立で、関数
が独立で、関数 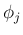 により
により
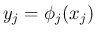 というあらたな確率変数が作られるとき、
というあらたな確率変数が作られるとき、
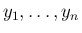 も (
も (
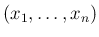 の
の 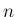 次元確率分布の
元で) 独立となる。
次元確率分布の
元で) 独立となる。
この命題の「あらたな確率変数が作られるとき」という表現については、
連続確率変数の場合は任意の関数であらたな連続確率変数が
作られるとは限らないために用いている。
例えば、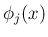 が
が 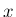 の 1 次式、多項式などであれば問題はない。
詳しくは、[1] を参照のこと。
の 1 次式、多項式などであれば問題はない。
詳しくは、[1] を参照のこと。
また、「
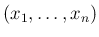 の
の 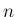 次元確率分布の元で」という
表現については、「
次元確率分布の元で」という
表現については、「
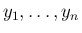 」の独立性は本来
」の独立性は本来
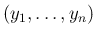 に関する
に関する 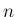 次元確率分布のとり方によって
決まることであるが、
それを「
次元確率分布のとり方によって
決まることであるが、
それを「
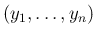 の
の 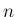 次元確率分布を
次元確率分布を
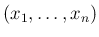 の
の 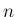 次元確率分布から自然に決まるものとする」、
すなわち、
次元確率分布から自然に決まるものとする」、
すなわち、
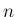 次元確率分布とその独立性については、
詳しくは、[1] を参照のこと。
次元確率分布とその独立性については、
詳しくは、[1] を参照のこと。
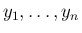 が独立であることは、任意の
が独立であることは、任意の 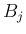 に対し
に対し
![[*]](crossref.png) )、
および
)、
および
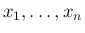 が独立であるという仮定により、
(
が独立であるという仮定により、
(![[*]](crossref.png) ) の左辺は
) の左辺は
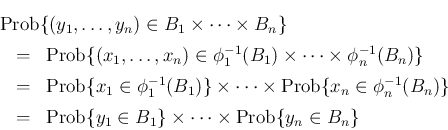
![[*]](crossref.png) ) が成立する。
) が成立する。
命題 ![[*]](crossref.png) の正規分布に従う確率変数
の正規分布に従う確率変数 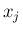 に対して 標準化
に対して 標準化
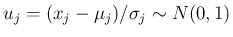 を取れば、
命題
を取れば、
命題 ![[*]](crossref.png) より
より
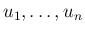 は独立で、
は独立で、
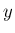 は、
は、
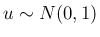 ならば
ならば
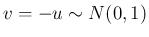
証明
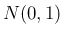 の密度関数
の密度関数
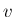 の分布関数
の分布関数
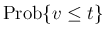 は、
は、
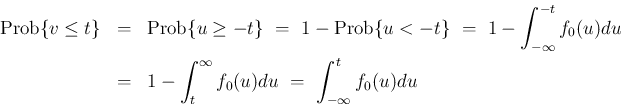
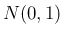 の分布関数に一致する。
の分布関数に一致する。
よって、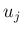 に対して
に対して
![[*]](crossref.png) により
により
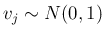 で、
命題
で、
命題 ![[*]](crossref.png) より
より
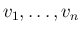 も独立であり、
また
も独立であり、
また
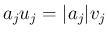 となるので、(
となるので、(![[*]](crossref.png) ) は、
と書ける。つまり、命題
) は、
と書ける。つまり、命題 ![[*]](crossref.png) を、
を、
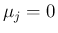 ,
, 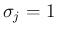 ,
, 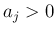 の形に帰着できることになる。
の形に帰着できることになる。
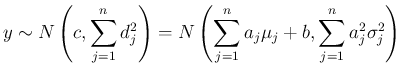
![[*]](crossref.png) が得られることがわかる。
よって後は、命題
が得られることがわかる。
よって後は、命題 ![[*]](crossref.png) を、
を、
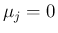 ,
, 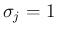 ,
, 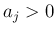 の元で示せばよい。
の元で示せばよい。
竹野茂治@新潟工科大学