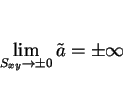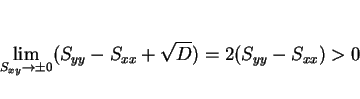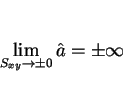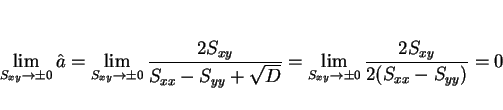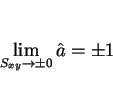

Next: 6 スケール変換に対する不変性
Up: 相関係数に関する一考察
Previous: 4 回転不変性について
(PDF ファイル: corel1.pdf)
5 点と直線の距離を用いた回帰直線
この節では、通常の回帰直線とは違い、
データ点と直線の距離の平方和を最小にする直線を求めることにする。
直線を 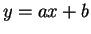 として、3 節と同様に行なう。
ただし、この場合は
として、3 節と同様に行なう。
ただし、この場合は 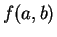 の代わりに
の代わりに
を考えることになる。
ところで、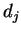 と
と
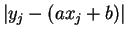 を比較すると、
直線の傾きが
を比較すると、
直線の傾きが 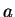 なので、
なので、
となり、よって
であることがわかる。
よって、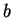 に関する最小値は 3 節の計算と同じで、
に関する最小値は 3 節の計算と同じで、
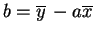 のときにとる。
その最小値
のときにとる。
その最小値 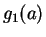 は
は
となる。この分数関数の最小値を求めれば良い。微分すると、
となる。この分子の 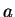 に関する 2 次式は、判別式が
に関する 2 次式は、判別式が
となるので、
と書ける。ここで、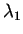 ,
, 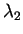 は
は
であり、これにより、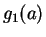 の微分は
の微分は
となる。
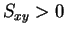 のとき
のとき
このとき、
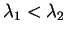 であり、よって最小値は
であり、よって最小値は
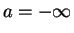 か
か 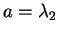 で取る。
で取る。
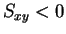 のとき
のとき
このときは、
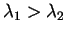 であるが、
であるが、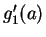 には
には
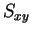 がかかっているので、最小値は
がかかっているので、最小値は
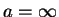 か
か 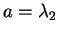 で取る。
で取る。
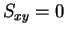 のとき
のとき
このときは、
より、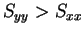 ならば
ならば 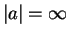 のときに最小値
のときに最小値 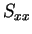 を、
を、
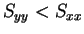 ならば
ならば 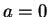 のときに最小値
のときに最小値 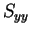 を、
を、
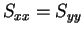 ならばつねに
ならばつねに 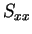 に等しい値を取る。
に等しい値を取る。
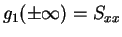 であるから、
次は
であるから、
次は 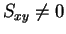 のときに、これと
のときに、これと
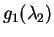 とを比較する。
とを比較する。
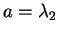 は
は
の解なので
となる。これにより、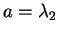 に対し、
に対し、
となるが、
より、
となる。ここで、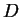 の定義より、
の定義より、
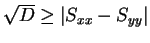 (等号は
(等号は 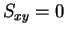 ) であるので、
) であるので、
は、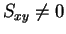 のとき、確かに
のとき、確かに 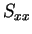 より小さく、
よってこれが最小値となる。
より小さく、
よってこれが最小値となる。
結局、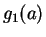 の最小値は以下のようになる。
の最小値は以下のようになる。
この 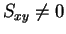 のときの最小値
のときの最小値
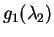 は、
以下のように書き換えることができる。
は、
以下のように書き換えることができる。
ここで、
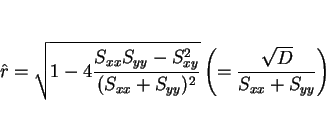 |
(5) |
とすると、最小値
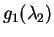 は
は
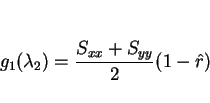 |
(6) |
と書ける。
なお、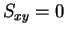 の場合、
の場合、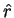 は
は
となるので、
となり、式 (6) は
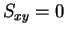 の場合も最小値を与えていることになる。
の場合も最小値を与えていることになる。
この 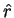 は、以下に述べるような色々な性質を持っている。
は、以下に述べるような色々な性質を持っている。
以上のことから、ある意味ではむしろ 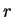 よりも優れている性質を持つ、
あらたな「相関係数」
よりも優れている性質を持つ、
あらたな「相関係数」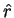 が得られたことになる。
相関係数として
が得られたことになる。
相関係数として 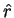 を使えば、問題 1 もある意味で解決する。
を使えば、問題 1 もある意味で解決する。
また、上で得られた「回帰直線」の傾き
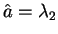 も、
もちろん回転不変性 (すなわちデータの回転に合わせて直線も同じだけ回転)
を持ち、
も、
もちろん回転不変性 (すなわちデータの回転に合わせて直線も同じだけ回転)
を持ち、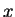 ,
, 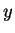 の入れ替えにも対応することが、その定義からすぐに分かる。
さらに次も言える。
の入れ替えにも対応することが、その定義からすぐに分かる。
さらに次も言える。
命題 1
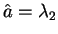 ,
,
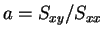 , および
データの
, および
データの 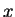 ,
,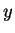 を入れ替えて作った回帰直線を
を入れ替えて作った回帰直線を 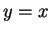 に関して
対称に折り返した直線の傾き
に関して
対称に折り返した直線の傾き
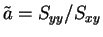 (cf. 4 節) に対して次が成り立つ。
(cf. 4 節) に対して次が成り立つ。
なお、4 つの不等号の等号成立は、いずれも完全な直線相関のとき (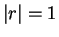 )。
)。
証明
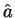 は、
は、
なので、
で、
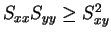 より
より 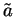 と
と 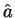 の大小関係が得られる。そして等号成立は
の大小関係が得られる。そして等号成立は
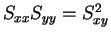 、すなわち
、すなわち
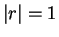 のときであることもわかる。
のときであることもわかる。
また、
であり、
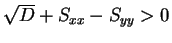 より
より 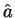 と
と 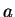 の大小関係が得られる。等号成立はこちらも
の大小関係が得られる。等号成立はこちらも
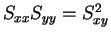 の場合となる。
の場合となる。
なお、
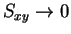 のときは、
のときは、
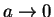 ,
, 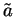 は
は
であるが、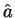 は、
は、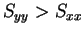 のときは
のときは
なので
であり、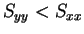 のときは
のときは
となる。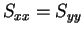 のときは、
のときは、
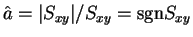 より、
より、
となる。
以上が問題 3 の前半部分に対する答えとなる。


Next: 6 スケール変換に対する不変性
Up: 相関係数に関する一考察
Previous: 4 回転不変性について
Shigeharu TAKENO
2004年 10月 18日
![]() として、3 節と同様に行なう。
ただし、この場合は
として、3 節と同様に行なう。
ただし、この場合は ![]() の代わりに
の代わりに
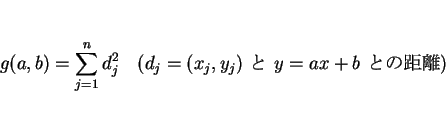
![]() と
と
![]() を比較すると、
直線の傾きが
を比較すると、
直線の傾きが ![]() なので、
なので、
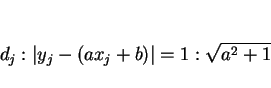
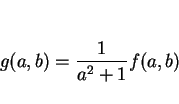
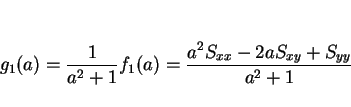
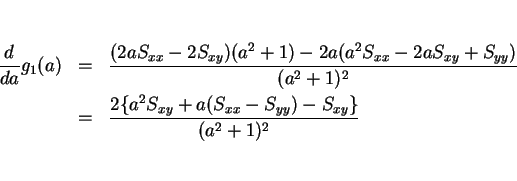
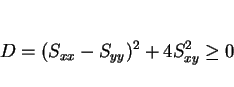
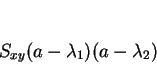
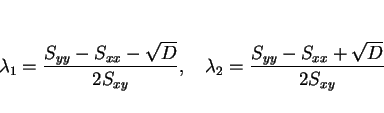
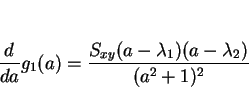
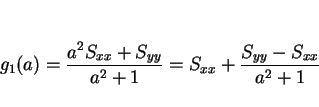
![]() であるから、
次は
であるから、
次は ![]() のときに、これと
のときに、これと
![]() とを比較する。
とを比較する。
![]() は
は
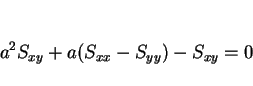
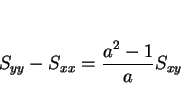
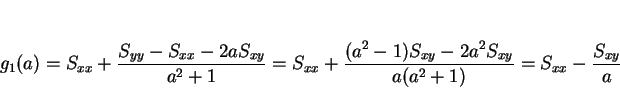
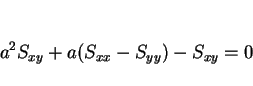
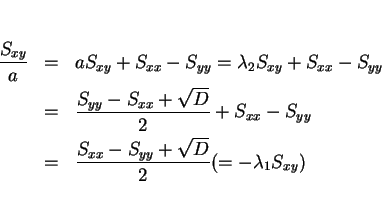
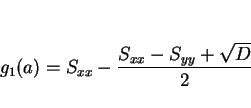
![]() の最小値は以下のようになる。
の最小値は以下のようになる。
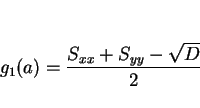
![]() のときの最小値
のときの最小値
![]() は、
以下のように書き換えることができる。
は、
以下のように書き換えることができる。
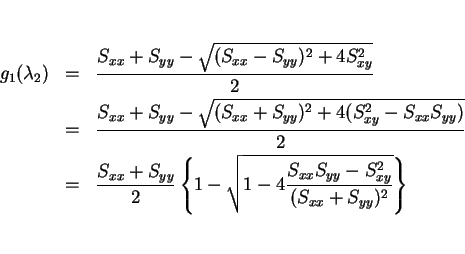
![]() の場合、
の場合、![]() は
は
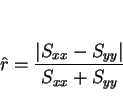
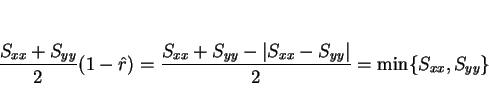
![]() は、以下に述べるような色々な性質を持っている。
は、以下に述べるような色々な性質を持っている。
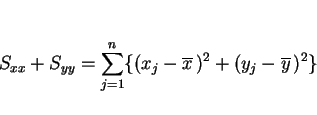
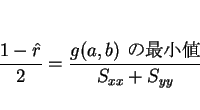
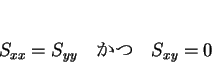
![]() のときには
のときには ![]() しか得られないが、
しか得られないが、
![]() の場合はそれに加えて
の場合はそれに加えて ![]() も得られるので、
も得られるので、
![]() よりもやや強いことが言えるのである。
よりもやや強いことが言えるのである。
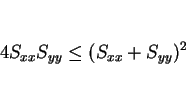
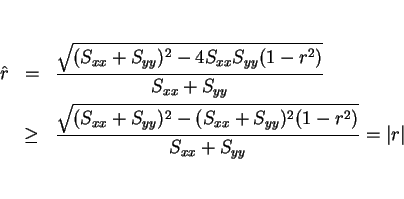
![]() も、
もちろん回転不変性 (すなわちデータの回転に合わせて直線も同じだけ回転)
を持ち、
も、
もちろん回転不変性 (すなわちデータの回転に合わせて直線も同じだけ回転)
を持ち、![]() ,
, ![]() の入れ替えにも対応することが、その定義からすぐに分かる。
さらに次も言える。
の入れ替えにも対応することが、その定義からすぐに分かる。
さらに次も言える。
![]() ,
,
![]() , および
データの
, および
データの ![]() ,
,![]() を入れ替えて作った回帰直線を
を入れ替えて作った回帰直線を ![]() に関して
対称に折り返した直線の傾き
に関して
対称に折り返した直線の傾き
![]() (cf. 4 節) に対して次が成り立つ。
(cf. 4 節) に対して次が成り立つ。
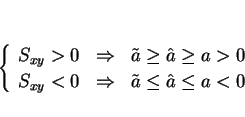
![]() は、
は、
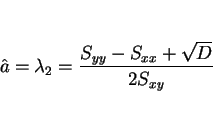
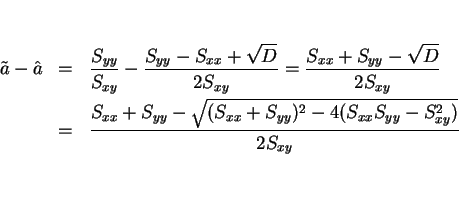
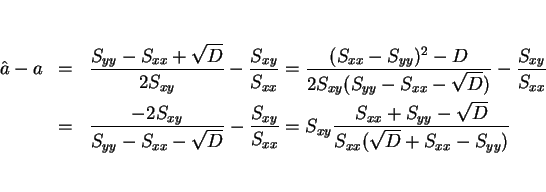
![]() のときは、
のときは、
![]() ,
, ![]() は
は