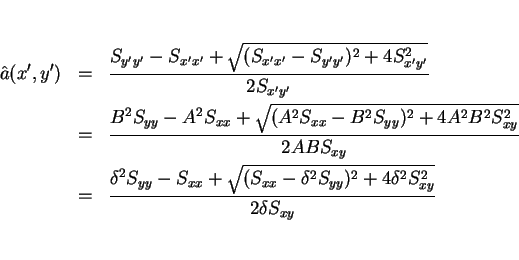

Next: 7 最後に
Up: 相関係数に関する一考察
Previous: 5 点と直線の距離を用いた回帰直線
(PDF ファイル: corel1.pdf)
6 スケール変換に対する不変性
データの指標としては、スケール変換に対する不変性も重要な性質である。
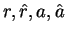 等について、これも調べてみる。
等について、これも調べてみる。
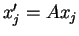 ,
, 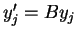 (
(
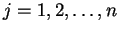 ,
, 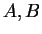 は正の定数) とすると、
は正の定数) とすると、
となることが容易に分かる。よって、
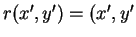 に対する
に対する 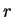 の値) 等とすると、
の値) 等とすると、
となり、通常の相関係数はこのスケール変換に対しては不変であることが分かる。
一方、新たに作った 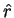 の方は、
の方は、
となり、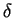 が 1 以外のときは明らかに
が 1 以外のときは明らかに 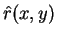 とは等しくならない。
つまり
とは等しくならない。
つまり 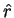 はこのスケール変換に関しては不変ではないことが分かる。
はこのスケール変換に関しては不変ではないことが分かる。
同様に回帰直線についても同じスケール変換を考えてみると、
通常の回帰直線は 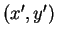 については
については
であるが、これは
となるので、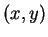 座標系では
座標系では
となり 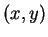 での回帰直線に一致する。つまり、一見
での回帰直線に一致する。つまり、一見
となり、スケール変換で変わってしまうようにも見えるが、
実際は本質的にスケール変換不変であることが分かる。
ところが、新たに考えた 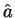 を用いた回帰直線の方は、
を用いた回帰直線の方は、
となり、これもやはり
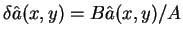 には一致せず、
本質的にこのスケール変換で変わってしまうことになる。
には一致せず、
本質的にこのスケール変換で変わってしまうことになる。


Next: 7 最後に
Up: 相関係数に関する一考察
Previous: 5 点と直線の距離を用いた回帰直線
Shigeharu TAKENO
2004年 10月 18日
![]() ,
, ![]() (
(
![]() ,
, ![]() は正の定数) とすると、
は正の定数) とすると、
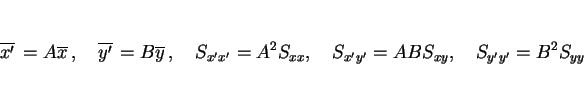
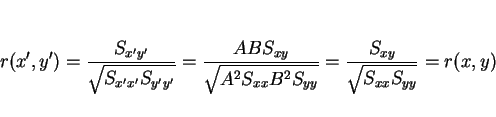
![]() の方は、
の方は、
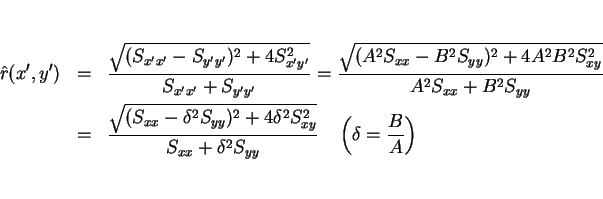
![]() については
については
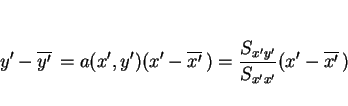
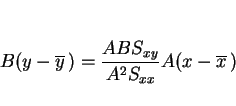
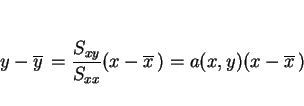
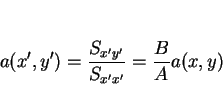
![]() を用いた回帰直線の方は、
を用いた回帰直線の方は、