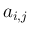
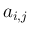 に
関する条件に書き直す。この式に (7) を代入すれば、
となり、両辺とも
に
関する条件に書き直す。この式に (7) を代入すれば、
となり、両辺とも
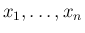 の 2 次式なので、
それが恒等式となるような係数の条件が求める条件となる。
の 2 次式なので、
それが恒等式となるような係数の条件が求める条件となる。
まずは、(14) の左辺 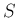 を計算する。
展開すると、
を計算する。
展開すると、
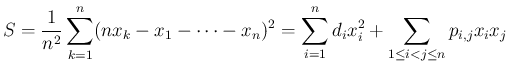
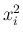 の係数
の係数 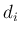 は、和の部分から出てくるのは、
は、和の部分から出てくるのは、
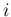 番目が
番目が 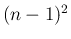 , それ以外の
, それ以外の 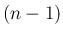 個は 1 なので、
個は 1 なので、
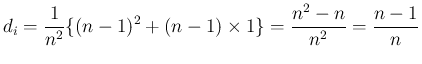
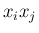 の係数
の係数 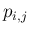 は、和の部分から出てくるのは、
は、和の部分から出てくるのは、
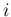 番目と
番目と 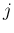 番目が
番目が 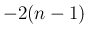 、それ以外の
、それ以外の 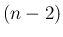 個は 2 なので、
個は 2 なので、
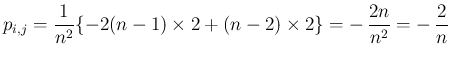
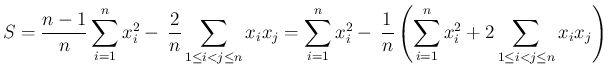
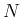 , 列ベクトル
, 列ベクトル
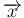 を
とすると、対称行列
を
とすると、対称行列 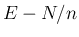 に関する 2 次形式
の形に書くことができる。
に関する 2 次形式
の形に書くことができる。
一方、(14) の右辺 (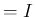 とする) は、
とする) は、
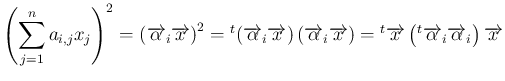
![$\displaystyle Q
= \sum_{i=1}^{n-1}{}^t{\overrightarrow{\alpha}_i}\overrightarro...
...ightarrow{\alpha}_1\\ \vdots\\ \overrightarrow{\alpha}_{n-1}\end{array}\right]
$](img64.png)
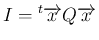
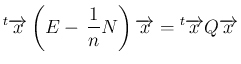
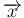 に関して恒等的に成り立つためには、
に関して恒等的に成り立つためには、
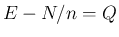 が条件となる。
が条件となる。
一方、
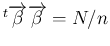 となるので、
となるので、
![$\displaystyle Q+\frac{1}{n}N
= \sum_{i=1}^{n-1}{}^t{\overrightarrow{\alpha}_i}...
...rrightarrow{\alpha}_{n-1}\\ \overrightarrow{\beta}\end{array}\right]
={}^t{A}A
$](img69.png)
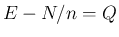 は
は 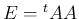 と同じことになり、
そしてこれは (13) とも等しい。
と同じことになり、
そしてこれは (13) とも等しい。
すなわち、正規性と独立性の条件 (13) によって、
(14) も自動的に得られることになり、
結局 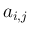 の満たすべき条件は
の満たすべき条件は 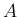 が直交行列になること、となる。
が直交行列になること、となる。
これを満たす 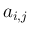 はたくさんある。例えば、
はたくさんある。例えば、
 で紹介した例 (4), (5) も
ほぼこの解と同じで、
で紹介した例 (4), (5) も
ほぼこの解と同じで、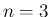 の方は
の方は 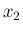 と
と 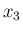 を入れかえて、
を入れかえて、
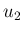 を
を 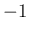 倍すれば上の形になる。
倍すれば上の形になる。
以上により、一般の 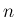 (
(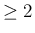 ) に対して (3) が示されたことになる。
) に対して (3) が示されたことになる。
竹野茂治@新潟工科大学