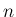
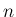 のカイ自乗分布
のカイ自乗分布 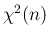 は、
は、
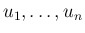 が
が 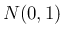 に従う確率変数で、かつ独立であるとき、
が従う確率分布である。
に従う確率変数で、かつ独立であるとき、
が従う確率分布である。
本稿で証明するのは、
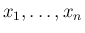 を正規母集団から取ったデータ、
すなわち
を正規母集団から取ったデータ、
すなわち 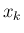 が
が
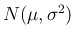 に従う確率変数でかつ
それらが独立であるとき、標本平均
に従う確率変数でかつ
それらが独立であるとき、標本平均 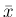 , 平方和
, 平方和 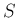
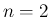 のときは
のときは
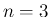 のときは
によって
と書け、かつ
のときは
によって
と書け、かつ
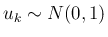 でかつ
でかつ
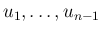 が
独立であることを講義では紹介した (が、証明はしていない)。
が
独立であることを講義では紹介した (が、証明はしていない)。
これと同様に、一般の 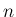 に対しても、
(6) となるような
に対しても、
(6) となるような 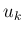 を、
を、
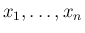 の 1 次式として構成し、それが独立でかつ
の 1 次式として構成し、それが独立でかつ 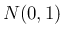 に
従うことを示すことで (3) を示す。
に
従うことを示すことで (3) を示す。
竹野茂治@新潟工科大学