2 用語
まずこの節では、前節でも出てきた用語等について確認しておく。
詳しくは、適当な微分の教科書 (偏微分の部分) を参照すること。
また、以後 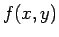 は、すべての実数
は、すべての実数 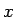 ,
, 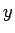 について定義されていて、
十分滑らかであるとする。
について定義されていて、
十分滑らかであるとする。
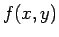 が
が 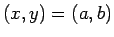 で 極大 (極小) であるとは、
で 極大 (極小) であるとは、
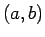 の十分近くの
の十分近くの 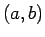 とは異なるすべての
とは異なるすべての 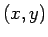 に対して
に対して
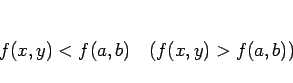
となることを言う。
また、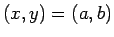 で 最大 (最小) であるとは、
すべての
で 最大 (最小) であるとは、
すべての 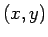 に対して、
に対して、
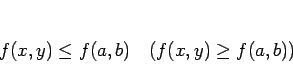
であることを言う。
1 変数の場合と同じで極大、極小は局所的な性質であり、
最大、最小は大域的な性質である。
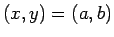 が
が 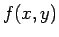 の 停留点 であるとは、
の 停留点 であるとは、
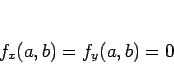
が成り立つことを言う。これは 1 変数関数の場合の 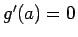 に相当し、
このような点が極の候補となる。
に相当し、
このような点が極の候補となる。
極の判別は、凸性を調べることで行うことができ、それについては
たいていの教科書に書いてある次の事実を用いる。
命題 1
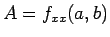 ,
, 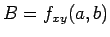 ,
, 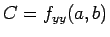 とするとき、
とするとき、
-
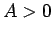 かつ
かつ 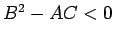 ならば
ならば
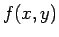 は
は 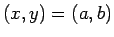 で下に凸 (すなわち、
で下に凸 (すなわち、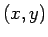 平面のどの方向に対しても下に凸)
平面のどの方向に対しても下に凸)
-
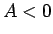 かつ
かつ 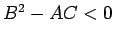 ならば
ならば
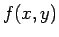 は
は 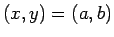 で上に凸 (すなわち、
で上に凸 (すなわち、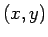 平面のどの方向に対しても上に凸)
平面のどの方向に対しても上に凸)
-
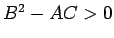 ならば方向によって
凸性が入れ変わる
ならば方向によって
凸性が入れ変わる
よって、まず停留点を求め、
そしてそこでの 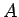 ,
, 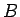 ,
, 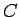 の値を求めて、
の値を求めて、
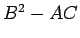 と
と 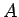 の符号で極の判別をする、というのが
標準的な方法であり、停留点では、
命題 1 の 1. であれば極小、
2. であれば極大、
そして 3. であれば
極ではない (鞍点 と呼ばれる) ことが言えることになる。
の符号で極の判別をする、というのが
標準的な方法であり、停留点では、
命題 1 の 1. であれば極小、
2. であれば極大、
そして 3. であれば
極ではない (鞍点 と呼ばれる) ことが言えることになる。
竹野茂治@新潟工科大学
2008年12月14日
![]() が
が ![]() で 極大 (極小) であるとは、
で 極大 (極小) であるとは、
![]() の十分近くの
の十分近くの ![]() とは異なるすべての
とは異なるすべての ![]() に対して
に対して
![]() が
が ![]() の 停留点 であるとは、
の 停留点 であるとは、
![]() ,
, ![]() ,
, ![]() とするとき、
とするとき、
![]() ,
, ![]() ,
, ![]() の値を求めて、
の値を求めて、
![]() と
と ![]() の符号で極の判別をする、というのが
標準的な方法であり、停留点では、
命題 1 の 1. であれば極小、
2. であれば極大、
そして 3. であれば
極ではない (鞍点 と呼ばれる) ことが言えることになる。
の符号で極の判別をする、というのが
標準的な方法であり、停留点では、
命題 1 の 1. であれば極小、
2. であれば極大、
そして 3. であれば
極ではない (鞍点 と呼ばれる) ことが言えることになる。