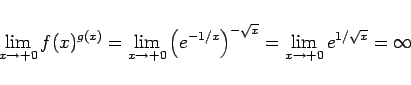次へ: この文書について...
上へ: xtothex1
前へ: 1 x の x 乗の微分
(PDF ファイル: xtothex1.pdf)
ごくたまに、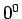 は 0 ですか、と聞かれることがある。
実際には不定形なので、
は 0 ですか、と聞かれることがある。
実際には不定形なので、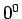 と書かれると何とも答えようがないが、
と書かれると何とも答えようがないが、
ならば極限を持つ。これは次のようにして求めることができる。
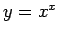 の極限を考える代わりに
の極限を考える代わりに
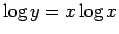 の極限を考える。すると
ロピタルの定理により
の極限を考える。すると
ロピタルの定理により
となるので、
となる。
古い話になるが、私が大学 1 年のときの解析のテスト問題の一つに、
この極限をロピタルの定理を「用いずに」求めよ、という問題が出たことがある。
興味のある人は考えてみるといいだろう。
(追記)
上記をもって、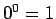 と誤解してはいけない。最初にも述べたように、
と誤解してはいけない。最初にも述べたように、
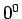 は不定形であって 1 ではない。
すなわち、
は不定形であって 1 ではない。
すなわち、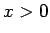 で定義された関数
で定義された関数 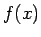 ,
, 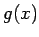 が
が
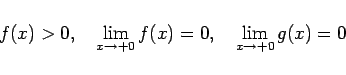 |
(1) |
を満たす場合に、
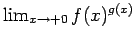 の値は一定値には収束しない (上に紹介したのは、単に
の値は一定値には収束しない (上に紹介したのは、単に 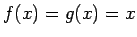 の場合の話)。
例えば、
の場合の話)。
例えば、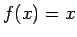 ,
, 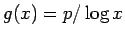 (
(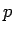 は 0 以外の定数) とすれば
これは (1) を満たすが、
は 0 以外の定数) とすれば
これは (1) を満たすが、
すなわち
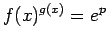 であるから、
であるから、
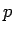 により 1 以外の任意の正の値を取りうる。
により 1 以外の任意の正の値を取りうる。
また、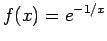 ,
,
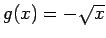 とすればこれも (1) を満たすが、
とすればこれも (1) を満たすが、
のように 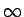 にもなりうる。
よって
にもなりうる。
よって 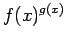 の値は一つには決まらず、
の値は一つには決まらず、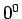 は不定形である。
は不定形である。
次へ: この文書について...
上へ: xtothex1
前へ: 1 x の x 乗の微分
竹野茂治@新潟工科大学
2006年3月5日
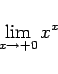
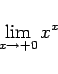
![]() の極限を考える代わりに
の極限を考える代わりに
![]() の極限を考える。すると
ロピタルの定理により
の極限を考える。すると
ロピタルの定理により
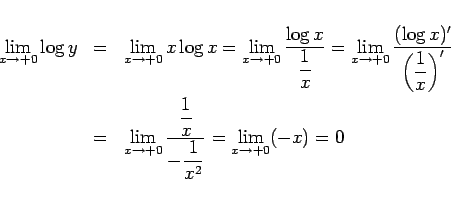
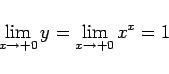
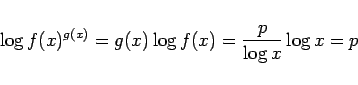
![]() ,
,
![]() とすればこれも (1) を満たすが、
とすればこれも (1) を満たすが、