次へ: 2 0 の 0 乗
上へ: xtothex1
前へ: xtothex1
(PDF ファイル: xtothex1.pdf)
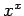 の微分は、底も指数も定数でないので、通常の
の微分は、底も指数も定数でないので、通常の 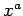 や
や
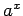 の微分の公式が使えずやや難しい。通常は
の微分の公式が使えずやや難しい。通常は
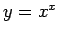 とおいて両辺の対数をとり
とおいて両辺の対数をとり
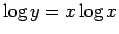 として
両辺を微分 (対数微分法)
として
両辺を微分 (対数微分法)
-
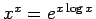 と変形して微分
と変形して微分
のいずれかを使うのではないかと思われる。
ここでは、例年基礎数理 III で紹介している 2 変数関数の合成関数の微分法:
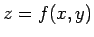 に
に 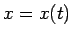 ,
, 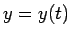 を代入した
を代入した
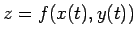 に対して、
に対して、
を用いる方法を紹介する1。
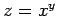 とすると、
とすると、
となるので、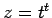 を
を 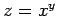 に
に 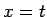 ,
, 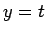 を代入したものと考えれば
2 変数関数の合成関数の微分法により
を代入したものと考えれば
2 変数関数の合成関数の微分法により
となり、よって
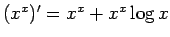 が得られる。
が得られる。
この方法のいいところは、常微分の範疇ではこの関数には使えない
通常の 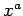 や
や 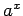 の微分の公式が、偏微分では使える、という点にある。
の微分の公式が、偏微分では使える、という点にある。
ただし、もちろん偏微分をやった後でないと学生には紹介できない。
次へ: 2 0 の 0 乗
上へ: xtothex1
前へ: xtothex1
竹野茂治@新潟工科大学
2006年3月5日
に
,
を代入した
に対して、
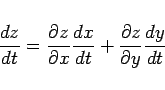
![]() とすると、
とすると、
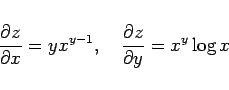
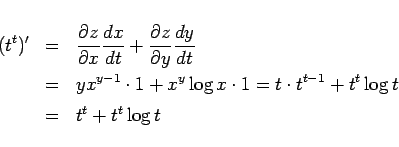
![]() や
や ![]() の微分の公式が、偏微分では使える、という点にある。
の微分の公式が、偏微分では使える、という点にある。