5 より小さい勾配への帰着
3 節で述べたように、
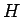 が 1 以下というだけではまだ不十分なので、
より小さな
が 1 以下というだけではまだ不十分なので、
より小さな 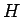 に帰着させることを考える。
に帰着させることを考える。
4 節と同様にして、次は
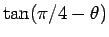 を考える。
加法定理 (5) により、
を考える。
加法定理 (5) により、
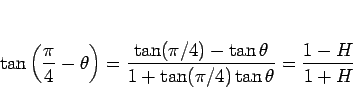
なので、
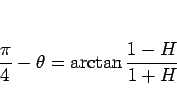 |
(7) |
が得られる。
よって、今度は 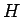 と
と 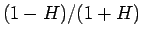 の小さい方を使えることになる。
の小さい方を使えることになる。
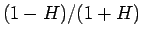 は
は 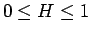 に対して 1 から 0 に単調減少し、
に対して 1 から 0 に単調減少し、
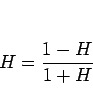
となる 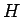 はこの範囲では
はこの範囲では 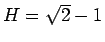 のみである。よって、
のみである。よって、
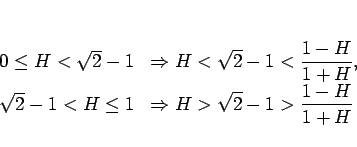
となり、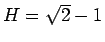 を境に分かれることになる。
なお、丁度
を境に分かれることになる。
なお、丁度 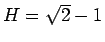 のときは、
のときは、
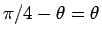 であり、よって
であり、よって 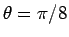 となる。
となる。
結局、
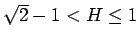 のときは、
のときは、
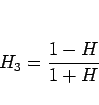
に対して
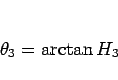
とすれば
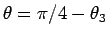 と求めることができるので、
これで
と求めることができるので、
これで 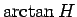 の計算は
の計算は
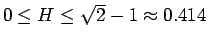 の場合に帰着されることになる。
の場合に帰着されることになる。
なお、実際のプログラムでは、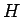 と
と 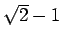 とを比較する代わりに
とを比較する代わりに
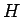 と
と 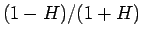 とを比較するようにすれば、
とを比較するようにすれば、
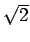 のような無理数の値を保持しておく必要はなくなる。
のような無理数の値を保持しておく必要はなくなる。
ここまでの考察によって、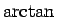 の展開式 (1) は
の展開式 (1) は
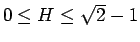 に対して使えばいいことになるので、
例えば (1) の最初の 4 項
に対して使えばいいことになるので、
例えば (1) の最初の 4 項
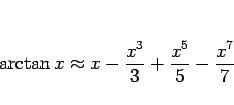
を使うのであれば、その誤差はその次の項 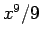 にほぼ等しく、
よってその最大誤差は
にほぼ等しく、
よってその最大誤差は
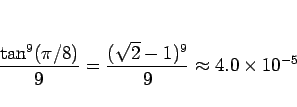 |
(8) |
程度ということになる。
竹野茂治@新潟工科大学
2009年1月18日
![]() を考える。
加法定理 (5) により、
を考える。
加法定理 (5) により、
![]() は
は ![]() に対して 1 から 0 に単調減少し、
に対して 1 から 0 に単調減少し、
![]() のときは、
のときは、
![]() と
と ![]() とを比較する代わりに
とを比較する代わりに
![]() と
と ![]() とを比較するようにすれば、
とを比較するようにすれば、
![]() のような無理数の値を保持しておく必要はなくなる。
のような無理数の値を保持しておく必要はなくなる。
![]() の展開式 (1) は
の展開式 (1) は
![]() に対して使えばいいことになるので、
例えば (1) の最初の 4 項
に対して使えばいいことになるので、
例えば (1) の最初の 4 項