6 さらに進めた場合
5 節で述べた、
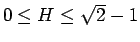 に帰着させる方法は、
まさに [1] の p41「逆三角関数」の項に書かれている内容であるが、
これをさらにもう一段進めるとどうなるであろうか。
に帰着させる方法は、
まさに [1] の p41「逆三角関数」の項に書かれている内容であるが、
これをさらにもう一段進めるとどうなるであろうか。
5 節の条件は
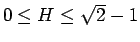 (
(
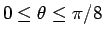 ) であるので、
) であるので、
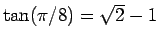 と加法定理 (5) を使えば、
と加法定理 (5) を使えば、
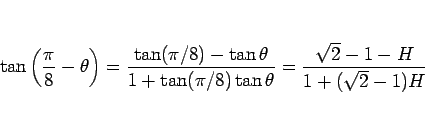
であるから、例えば
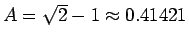 という定数を (必要な精度で) 保持しておけば、
という定数を (必要な精度で) 保持しておけば、
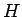 と
と
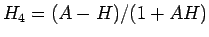 を比較し、
を比較し、
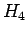 の方が小さい場合、
すなわち
の方が小さい場合、
すなわち
 の場合 (
の場合 (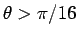 ) は、
) は、
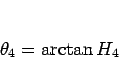
として 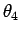 を求めて
を求めて
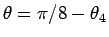 とすればよいので、
これで
とすればよいので、
これで
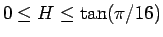 に帰着されることになる。
この
に帰着されることになる。
この 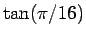 の値は、
の値は、 の半角の公式
の半角の公式
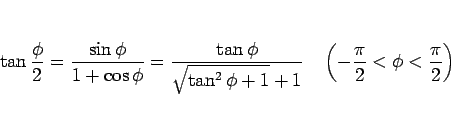 |
(9) |
を用いれば、
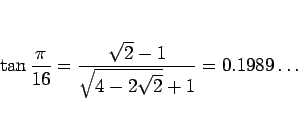
となるが、この二重根号は解消できないようである。
これに対する最大誤差は
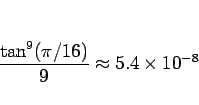 |
(10) |
なので、(8) より 3 桁ほど精度は上がることになる。
これと同等の精度を、この節の方法でなはく
近似和の項数を増やすことで出そうとすると、
5 節の
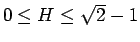 の範囲での最大誤差は
の範囲での最大誤差は
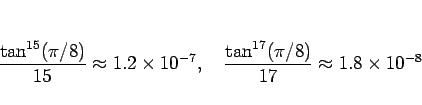
なので、7 項目までの和では足りず、
8 項目まで加えることでようやく本節の方法の精度を超えることになる。
ただし、実際にどちらが楽なのかは、それを計算する環境にもよるだろうから
一概にどちらとは断定できない。
なお、この節の方法は、
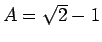 の値を定数として保持していればよいだけなので
平方根の計算をコンピュータで行う必要はない。
の値を定数として保持していればよいだけなので
平方根の計算をコンピュータで行う必要はない。
竹野茂治@新潟工科大学
2009年1月18日
![]() (
(
![]() ) であるので、
) であるので、
![]() と加法定理 (5) を使えば、
と加法定理 (5) を使えば、
![]() の範囲での最大誤差は
の範囲での最大誤差は
![]() の値を定数として保持していればよいだけなので
平方根の計算をコンピュータで行う必要はない。
の値を定数として保持していればよいだけなので
平方根の計算をコンピュータで行う必要はない。