3 正の勾配への帰着
本稿では、
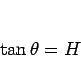 |
(2) |
を満たす 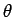 (
(
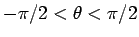 ) を求めることを考えることとする。
もちろん (2) は、
) を求めることを考えることとする。
もちろん (2) は、
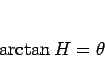 |
(3) |
と書くこともできるので、
これに (1) の展開式を用いれば良さそうであるが、
(1) は 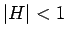 でないと使えないし、
でないと使えないし、
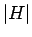 が 1 より小さくても 1 に近い場合は (1) は誤差が大きく、
精度を上げるにはかなり多くの項を取らなければいけない。
よって本稿では、三角関数の性質を用いることで、
この (1) をそれなりに小さな
が 1 より小さくても 1 に近い場合は (1) は誤差が大きく、
精度を上げるにはかなり多くの項を取らなければいけない。
よって本稿では、三角関数の性質を用いることで、
この (1) をそれなりに小さな 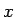 に対して用いれば
済むようにすることを考えていく。
に対して用いれば
済むようにすることを考えていく。
まず、正の勾配に帰着させることを考えよう。もし、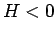 であれば、
であれば、
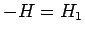 に対して
に対して
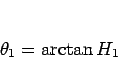
を求めれば、
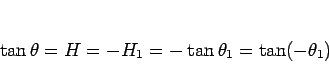
より
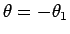 と求めることができるので、
アークタンジェントは 0 以上の勾配のみに対して使えばいいことになる。
言いかえれば、
と求めることができるので、
アークタンジェントは 0 以上の勾配のみに対して使えばいいことになる。
言いかえれば、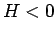 の場合は、
の場合は、
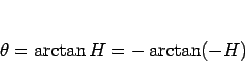
として求めれば良いことになる。
竹野茂治@新潟工科大学
2009年1月18日
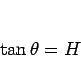
![]() であれば、
であれば、
![]() に対して
に対して