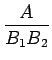 =
= 部分分数分解の原理は以下の通り。
多項式 B1(s) , B2(s) が互いに素で B(s) = B1(s)B2(s) であり、 deg A < deg B であれば、
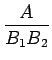 =
=
これにより、分母を因数分解すれば、 その因数に応じて互いに素な分母の分数に分解できることになる。 分子の A1 , A2 は未定係数法により求めることができる。 そして、分母の因数分解については、実数係数の多項式であれば、 次の定理により理論的には高々 2 次の因子にまで 実数の範囲で因数分解可能であることがわかる。
と 1 次因数の積に因数分解できる (代数学の基本定理)。
B(s) = a(s -) ... (s -
)
であるから、2. の共役な零点との因数を組み合わせることで 容易に得られる。 よって、重複する零点を重複度を含めて書くことにすれば、 B(s) は原理的には
(s -)(s -
) = (s - p - qi)(s - p + qi) = (s - p)2 + q2
| B(s) | = | a(s - r1)m1 ... (s - rL)mL x (s2 + |
|
| (mj |
| = | 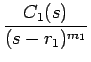 + ... + + ... + 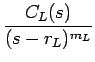 |
||
+ 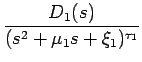 + ... + + ... + 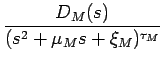 |
|||
| (deg Cj < mj, deg Dk < 2 |
の形の関数のラプラス逆変換を求められればよいことになる。
,
(deg C < m, deg D < 2
,
-4
< 0)
竹野茂治@新潟工科大学