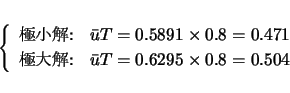
つまり,![]() の近くで 2 つの衝撃波を持つ 2 倍周期解が
起こるのは,1 周期毎にほぼ互いの衝撃波の位置が入れかわり,
それらがわずかにずれているためであると予想される.
その付近の
の近くで 2 つの衝撃波を持つ 2 倍周期解が
起こるのは,1 周期毎にほぼ互いの衝撃波の位置が入れかわり,
それらがわずかにずれているためであると予想される.
その付近の ![]() では極小解と極大解の存在により,
その両者を適当にまたぐことで平均値を調整できるので,
安定な周期解が存在する区間を保持できるのだろうと考えられる.
では極小解と極大解の存在により,
その両者を適当にまたぐことで平均値を調整できるので,
安定な周期解が存在する区間を保持できるのだろうと考えられる.
![]() の他にも,
の他にも,![]() ,
, ![]() などの近くでは
それぞれ 3 倍,5 倍の倍周期性が見られるので,
倍周期数はその移動速度 (特性速度) との関係が深いようである.
などの近くでは
それぞれ 3 倍,5 倍の倍周期性が見られるので,
倍周期数はその移動速度 (特性速度) との関係が深いようである.
一方,それらの区間外での ![]() に対しては,1 周期時間での
波の移動距離と
に対しては,1 周期時間での
波の移動距離と ![]() の有限区間長が簡単な整数比にならないので,
それにより 1 倍にもなりにくい,またはかなり大きな倍数の倍周期解に
まとまろうとしている,などの理由で不安定な状態に見えるのだろうと
予想される.
の有限区間長が簡単な整数比にならないので,
それにより 1 倍にもなりにくい,またはかなり大きな倍数の倍周期解に
まとまろうとしている,などの理由で不安定な状態に見えるのだろうと
予想される.
安定な倍周期解が,極小解と極大解をつなぐ衝撃波を持つ,
1 パラメータ族をなすことは
単独の保存則方程式特有の性質ではないかと思われる.
単独保存則方程式の場合,衝撃波 ![]() が満たすべき条件である
Rankine-Hugoniot 条件は
が満たすべき条件である
Rankine-Hugoniot 条件は
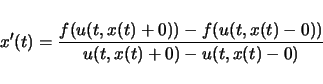
つまり,単独保存則方程式の場合,そのように容易に作れる衝撃波を利用して 平均を調節することが可能で,そのことがそのような解が安定でかつ現われやすい, という理由になっているのではないかと思われる.
連立方程式の場合は Rankine-Hugoniot 条件は複数の条件になり, それを衝撃波に対する常微分方程式と見ても過剰決定系になってしまい, 解の存在は明らかではなく特定の状況の元でしか解は存在し得ない. よって,そういう解が容易に安定なものとしては現われないのだろうと 考えられる.
また、今回得られた極小解と極大解は,丁度その接点の位置に関する 空間対称性を持っているように見える (Fig. 7). これは,2 倍周期解の場合だけでなく 3 倍周期解の極小解と極大解の組に 対しても見られる. それが,現在数値計算で用いている周期外力の空間対称性が原因なのか, それ以外の何らかの性質を表しているものなのかは今のところは不明であり, 今後それを検証する数値計算も必要であろうと考えられる.