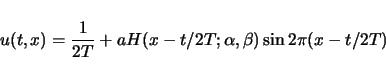 |
(7) |
連立の保存則方程式である気体の方程式の場合に得られた倍周期解の
![]() 毎の関数の形がかなり違っている[3]のに対して,
Burgers 方程式の数値計算で得られた数値的な倍周期解は,
いずれも
毎の関数の形がかなり違っている[3]のに対して,
Burgers 方程式の数値計算で得られた数値的な倍周期解は,
いずれも ![]() 毎の関数の形にあまり違いがなく[4],
毎の関数の形にあまり違いがなく[4],
もちろん,我々の手法,すなわち, 適当な初期値からスタートして解を先の方まで追いかけることで 漸近的な収束先としての周期解を得る という手法では全ての周期解を捕捉することができるわけではなく, 少なくとも数値的に安定なものしか得られないので, 上記の性質を持たない周期解が存在する可能性はある. 実際,定理 1 で構成した解は このような性質を持たない解である.
しかし,我々の手法で捕捉可能な安定な周期解は上記の性質を持つようであるので, それらが (7), (8), (9) のような構造から来るものなのかを検証するための数値実験を行なった. 目標は
を調べること,とした.
我々の手法では,同じ初期値からスタートすれば
同じ周期解にしか漸近し得ないので,
別な周期解を得るために,同じ平均値を持つ別な初期値を使って
その漸近収束先を追ってみた.その結果が Fig. 5,
6 である
(グラフはいずれも ![]() を,30 個分重ねたもの).
を,30 個分重ねたもの).
なお,この違いが ![]() に関する量子誤差によるものでないことは
確認済みであり,実際量子誤差よりも大きめの誤差を与えて
数値計算したところ,漸近形に対する影響は,Fig. 5,
6 の違いよりもごくわずかなものしか見られなかった.
に関する量子誤差によるものでないことは
確認済みであり,実際量子誤差よりも大きめの誤差を与えて
数値計算したところ,漸近形に対する影響は,Fig. 5,
6 の違いよりもごくわずかなものしか見られなかった.
さらに初期値を色々変えて実験を行なうと,衝撃波の位置の違うものが 色々得られ,それらが Fig. 5, 6 を含んで連続的に変形するような 1 パラメータの自由度を持つような族を 形成していることが確認できた.
次に,その周期解の集合の構造を調べるために,初期値は定数 (![]() ) に
して,その
) に
して,その ![]() の値を少しずつ変化させて極限の周期解を求めてみた.
それが Fig. 7-10 である
(グラフはいずれも
の値を少しずつ変化させて極限の周期解を求めてみた.
それが Fig. 7-10 である
(グラフはいずれも ![]() (
(![]() ) を重ねたもの).
) を重ねたもの).
![]() を細かくより連続的に変化させるとわかるが,
を細かくより連続的に変化させるとわかるが,
![]() =0.5891, 0.6295 では衝撃波のない 1 倍の周期解 (極小解,極大解)
が得られていて,その間の
=0.5891, 0.6295 では衝撃波のない 1 倍の周期解 (極小解,極大解)
が得られていて,その間の ![]() ではその両者を衝撃波でつないで
平均値を調整しているような倍周期解が現われる.
ではその両者を衝撃波でつないで
平均値を調整しているような倍周期解が現われる.
また,実際には ![]() =0.6089 付近で,極大解と極小解が接触するところで
交差するグラフを持つような,衝撃波を持たない滑らかな 1 倍周期解が
存在するようにも見えるが,正確には確認できていない.
=0.6089 付近で,極大解と極小解が接触するところで
交差するグラフを持つような,衝撃波を持たない滑らかな 1 倍周期解が
存在するようにも見えるが,正確には確認できていない.
その後,![]() を 0.6295 よりもさらに大きくした場合を調べてみたが,
しばらくはあまり漸近安定性の良くない 1 倍の周期解のようなもの
(前回の報告[4] 3 節の Fig. 2 参照) が現われ,
その後また新たな極小解と極大解を与える
を 0.6295 よりもさらに大きくした場合を調べてみたが,
しばらくはあまり漸近安定性の良くない 1 倍の周期解のようなもの
(前回の報告[4] 3 節の Fig. 2 参照) が現われ,
その後また新たな極小解と極大解を与える ![]() の値のペアが現われ
(例えば 0.728 と 0.739 や 0.805 と 0.827),
その間の
の値のペアが現われ
(例えば 0.728 と 0.739 や 0.805 と 0.827),
その間の ![]() ではその両者を衝撃波でつなぐ倍周期解が現われるよう
である.
ではその両者を衝撃波でつなぐ倍周期解が現われるよう
である.