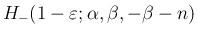
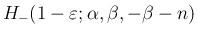 の
の
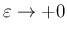 の
評価の精密化を行う。
これは、実は
の
評価の精密化を行う。
これは、実は 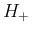 の展開式 (54) に近い形になる。
の展開式 (54) に近い形になる。
この場合も、(41) により、
は得られていたが、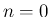 のときは、
反転公式 (18) と (43) により、
のときは、
反転公式 (18) と (43) により、
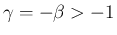 のときは
のときは
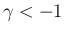 でも成立すること、
および
でも成立すること、
および
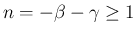 の場合の展開式
を
の場合の展開式
を 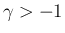 で得て、かつそれが
で得て、かつそれが 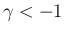 の場合にも
成立することを示すことが本節の目標である。
先に
の場合にも
成立することを示すことが本節の目標である。
先に 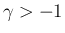 の (57) を考え、
そのあとで
の (57) を考え、
そのあとで 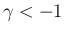 に対する (56) と (57) を考えることにする。
に対する (56) と (57) を考えることにする。
なお、(57) を求めるには、
上の (56) と同じように
反転公式 (18) と (54) を
用いる方法もあるが、
実はそれだと 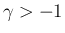 の場合でも簡単には式が得られない。
それは、
の場合でも簡単には式が得られない。
それは、
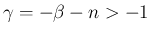 (
(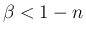 ) のとき、
反転公式 (18) と (44) を
用いて書き表してみると、
) のとき、
反転公式 (18) と (44) を
用いて書き表してみると、
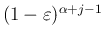 が残る和の部分で、
が残る和の部分で、
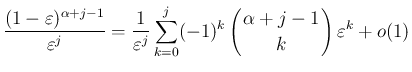
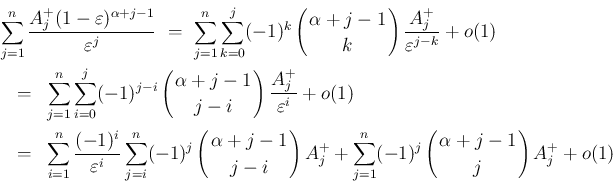
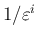 の係数が
の係数が 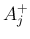 と二項係数の積の和になって、
それを求めるのが容易でないからである。
もちろん、最終形を予想した上で帰納法を用いる手段もあるが、
むしろ積分に戻って、
と二項係数の積の和になって、
それを求めるのが容易でないからである。
もちろん、最終形を予想した上で帰納法を用いる手段もあるが、
むしろ積分に戻って、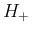 と同様の計算により導く方が早いので、
ここではその方針で考える。
と同様の計算により導く方が早いので、
ここではその方針で考える。
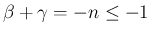 ,
,
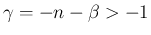 とする。
この場合、
とする。
この場合、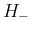 は、
は、
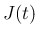 を用いて 2 つに分ける。
を用いて 2 つに分ける。
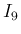 の積分のうち、
の積分のうち、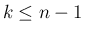 のものについては、
のものについては、
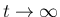 で可積分なので、
で可積分なので、

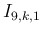 は
は
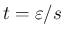 と置換すると、
と置換すると、
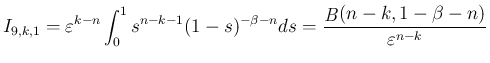
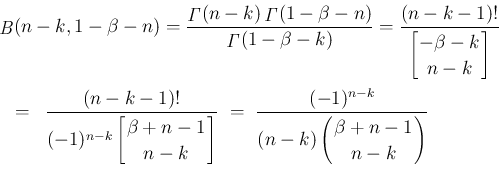
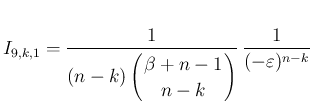
 は、ルベーグ収束定理により
は、ルベーグ収束定理により
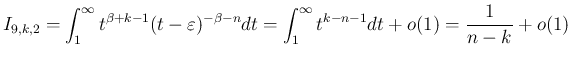
 に対しては、
に対しては、
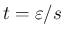 と置換すると、
と置換すると、
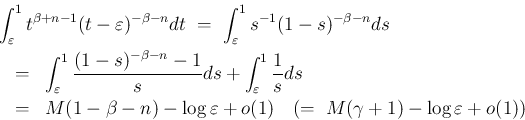
また、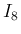 については、
については、
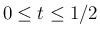 では
では
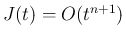 なので、
なので、
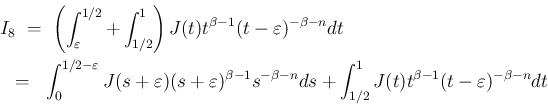
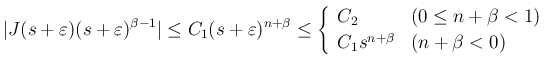
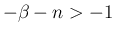 よりルベーグ収束定理が使えて、
よりルベーグ収束定理が使えて、
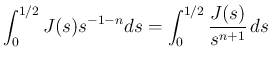
![$[1/2,1]$](img351.png) での積分に収束する。よって、
での積分に収束する。よって、
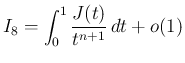
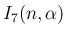 に等しいので、
補題 4 の 4. により
に等しいので、
補題 4 の 4. により
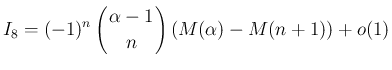
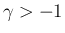 に対して、
補題 5 より、
に対して、
補題 5 より、
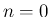 の (56) も含んでいる。
の (56) も含んでいる。
この 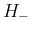 の展開式 (61) と
の展開式 (61) と 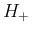 の展開式 (54) を比較すると、
の展開式 (54) を比較すると、
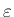 の負の巾の項が
の負の巾の項が  になっていることと、
定数項の部分の
になっていることと、
定数項の部分の 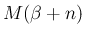 が
が 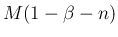 になっている
ところが違うだけで、他は全く同じ形になっていることがわかる。
になっている
ところが違うだけで、他は全く同じ形になっていることがわかる。
次は、この (61) が 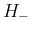 の
の 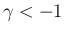 への拡張に対しても成り立つことを示す。
以後、(61) の係数を、
(57) のように
への拡張に対しても成り立つことを示す。
以後、(61) の係数を、
(57) のように
まずは 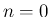 の場合、すなわち (56) が
の場合、すなわち (56) が
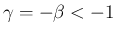 、すなわち
、すなわち 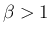 でも成立することを示す。
それには、(10) のリフティングと、
(41) の
でも成立することを示す。
それには、(10) のリフティングと、
(41) の
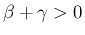 の評価を用いて、
の評価を用いて、
![$m=-[\gamma]$](img366.png) に関する帰納法により証明すればよい。
に関する帰納法により証明すればよい。
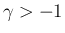 、すなわち
、すなわち 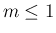 では (56) が
成り立っているので、
では (56) が
成り立っているので、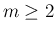 に対して (56) を
示せばよい。
今、
に対して (56) を
示せばよい。
今、![$-[\gamma]=m-1$](img368.png) までは (56) が
成り立つとする。
までは (56) が
成り立つとする。
![$-[\gamma]=m$](img369.png) に対しては、(10) を用いて
に対しては、(10) を用いて 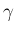 を一つ大きいもので表すと、
を一つ大きいもので表すと、
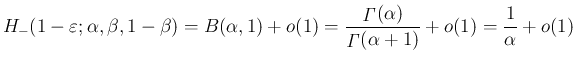
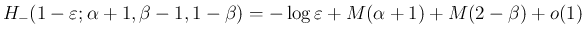
これで、帰納法により (56) が
すべての
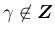 に対して成り立つことがわかる。
に対して成り立つことがわかる。
なお、この 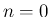 に対する証明を振り返ると、
に対する証明を振り返ると、
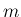 は実質的には使っておらず、(63) の
「
は実質的には使っておらず、(63) の
「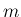 によらない」リフティングの式に、
「
によらない」リフティングの式に、
「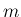 によらない」(41) の評価式と、
(56) の
によらない」(41) の評価式と、
(56) の 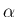 を
を 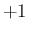 、
、
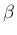 を
を 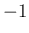 した式を代入して整理するだけの計算を行っている。
した式を代入して整理するだけの計算を行っている。
(56) は 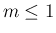 では
成立することがわかっているが、上の計算が「
では
成立することがわかっているが、上の計算が「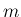 によらない」ので、
それに対しても同じ計算を行うことができて、
そして当然すでに成り立つことがわかっている結果が得られる。
だから、前の
によらない」ので、
それに対しても同じ計算を行うことができて、
そして当然すでに成り立つことがわかっている結果が得られる。
だから、前の 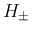 に対する性質 [i]
に対する性質 [i] [v] に対する証明と同じように、
[v] に対する証明と同じように、
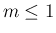 で「
で「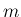 によらない計算」で成り立つことがわかることによって、
によらない計算」で成り立つことがわかることによって、
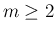 でも同じ計算によって成立することがわかることになる。
でも同じ計算によって成立することがわかることになる。
これは、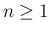 の場合の (62) でも同じ構造であり、
よって、それがすでに
の場合の (62) でも同じ構造であり、
よって、それがすでに 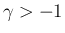 (
(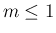 ) で成り立つこと
が示されていることによって、
) で成り立つこと
が示されていることによって、
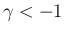 でも成り立つことが自然に示されることになるので、
これで (62) がすべての
でも成り立つことが自然に示されることになるので、
これで (62) がすべての 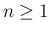 ,
,
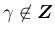 で成り立つことが言えることになる。
で成り立つことが言えることになる。
なお、もちろん、帰納法で 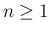 の場合の (62) を直接証明することも可能であり、
具体的には、
の場合の (62) を直接証明することも可能であり、
具体的には、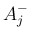 ,
, 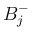 に対して、
に対して、
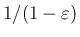 の
ためであり、この右辺をそのまま評価すると右辺の
の
ためであり、この右辺をそのまま評価すると右辺の
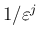 の係数は、
(58) と同様の計算により
いくつかの項の和になってしまうが、
逆に
の係数は、
(58) と同様の計算により
いくつかの項の和になってしまうが、
逆に
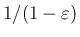 を (63) の左辺に回して
を (63) の左辺に回して
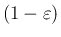 倍に変えてやると、
左辺の
倍に変えてやると、
左辺の
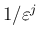 の同類項を 2 つの項だけの差にでき、
それが (65) の左辺である。
そしてそれにより証明を多少簡略化できる。
の同類項を 2 つの項だけの差にでき、
それが (65) の左辺である。
そしてそれにより証明を多少簡略化できる。
竹野茂治@新潟工科大学