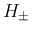
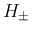 の
の
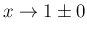 の評価を調べたが、
気体の方程式で必要な評価は、
の評価を調べたが、
気体の方程式で必要な評価は、
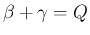 が整数の場合であり、
さらに
が整数の場合であり、
さらに 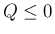 の場合は最悪の部分の評価だけでなく、
定数値までの展開が必要になる。
本節と次節で、
の場合は最悪の部分の評価だけでなく、
定数値までの展開が必要になる。
本節と次節で、
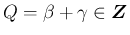 ,
, 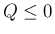 の場合に対して、
の場合に対して、
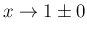 の評価のそのような精密化を行う。
の評価のそのような精密化を行う。
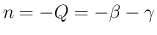 とし、本節では
とし、本節では
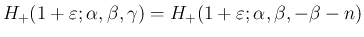
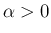 ,
, 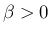 ,
,
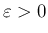 )。
今のところ、(40), および (39) により、
は得られている。この後者の
)。
今のところ、(40), および (39) により、
は得られている。この後者の 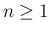 の方を、
の形に展開することが本節の目標である。
ここで
の方を、
の形に展開することが本節の目標である。
ここで 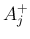 ,
, 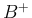 ,
, 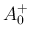 は
は 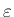 によらない定数。
なお、気体の方程式で必要なのは、
によらない定数。
なお、気体の方程式で必要なのは、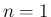 までであるが、
ここでは一般の自然数
までであるが、
ここでは一般の自然数 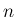 に対して考える。
に対して考える。
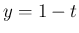 により、
により、
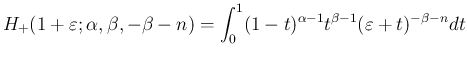
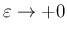 のときに
のときに 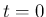 での order が
での order が 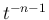 となってしまうので、このままでは極限が取れない。
よって、
となってしまうので、このままでは極限が取れない。
よって、
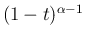 の部分を
の部分を 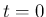 で展開して、
で展開して、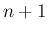 次に
なる項と多項式に分離する。すなわち、
とすると、
次に
なる項と多項式に分離する。すなわち、
とすると、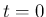 の近くでは
の近くでは
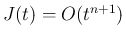 で、これにより、
で、これにより、
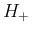 を以下の 2 つに分ける。
を以下の 2 つに分ける。
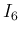 の各積分を考える。
の各積分を考える。
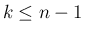 の場合、
の場合、
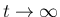 の order は
の order は 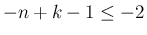 なので可積分であり、よって積分を
なので可積分であり、よって積分を
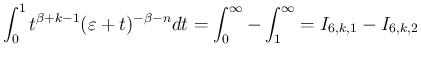
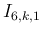 に対しては
に対しては
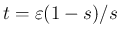 と置換すると
と置換すると
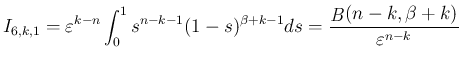
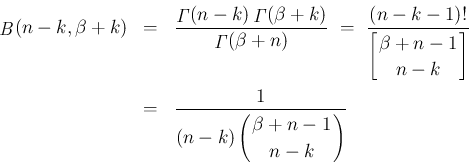
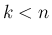 に対しては、
に対しては、
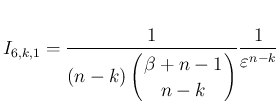
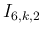 の方は、
の方は、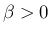 より
より
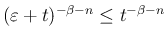 なので、ルベーグ収束定理より
なので、ルベーグ収束定理より
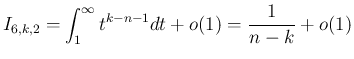
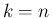 の項は、
の項は、
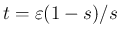 と置換すれば
と置換すれば
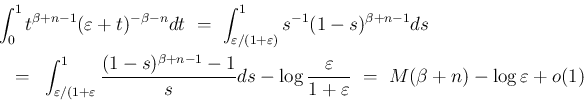
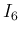 は、
は、
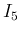 に関しては、
に関しては、
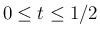 では
では
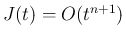 なので
ルベーグ収束定理により
なので
ルベーグ収束定理により
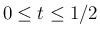 の積分はそのまま
の積分はそのまま
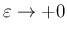 とできる。
また、
とできる。
また、
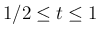 では
では
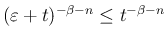 で、
で、
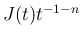 は可積分だから、やはりそのまま極限が取れる。
よって、
は可積分だから、やはりそのまま極限が取れる。
よって、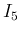 は
は
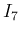 を求めればよい。
このあと使用するものを以下にまとめて補題として示す。
を求めればよい。
このあと使用するものを以下にまとめて補題として示す。
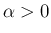 に対して、
に対して、
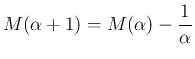
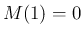
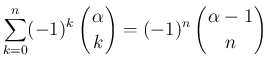
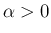 ,
, 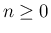 に対して、
に対して、
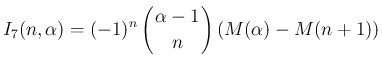
証明
1.
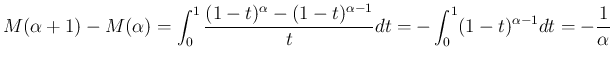
2. 定義 (38) より明らか。
3. 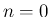 では成立し、
では成立し、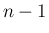 まで成立するとすると、
まで成立するとすると、
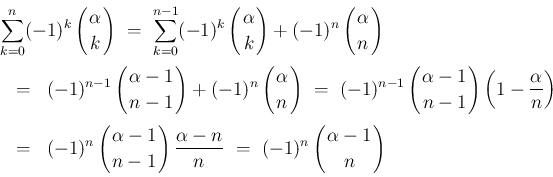
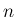 でも成立する。
でも成立する。
4.
以後、
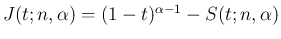 と
書くことにする。
と
書くことにする。
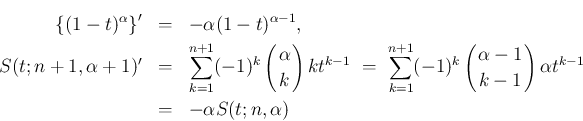
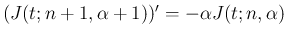 となるので、
部分積分により、
となるので、
部分積分により、
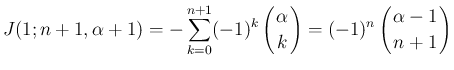
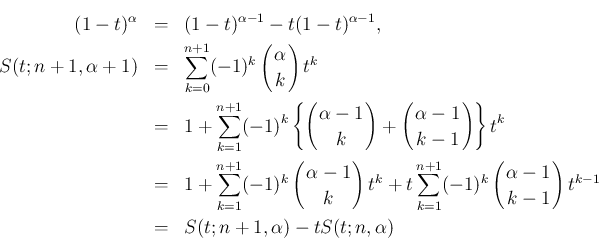
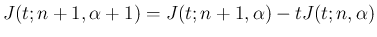
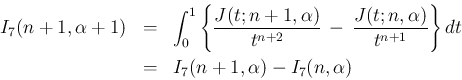
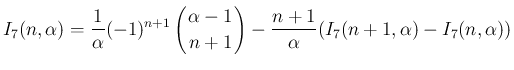
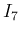 に関する漸化式
が得られる。
に関する漸化式
が得られる。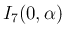 は、
は、
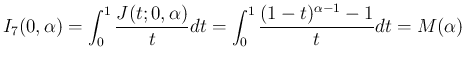
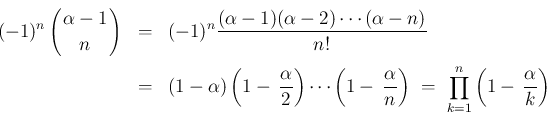
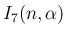 は、
は、
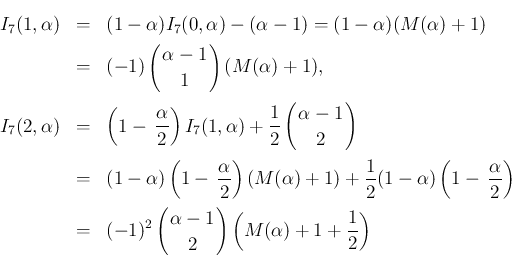
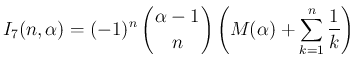
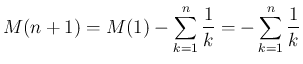
なお、この補題 4 の 1. により、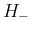 と同様に、
非整数の
と同様に、
非整数の 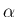 であれば、
であれば、
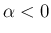 に対しても
に対しても
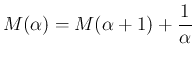
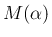 を拡張できることになり、以後そのように考える。
となるが、この定数部分は
を拡張できることになり、以後そのように考える。
となるが、この定数部分は 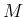 の拡張を用いれば、
さらに少しまとめられることを以下に示す。
の拡張を用いれば、
さらに少しまとめられることを以下に示す。
非整数の 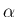 、および自然数
、および自然数 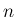 に対し、
に対し、
証明
補題 4 の 1. より
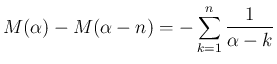
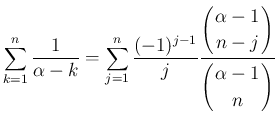
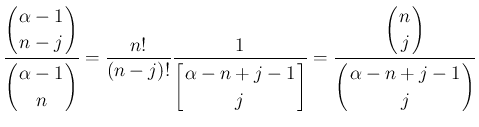
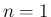 のときは、(53) の左辺は
のときは、(53) の左辺は 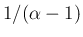 と
なるので成立する。
と
なるので成立する。
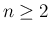 とし、
とし、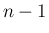 までは (53) が成立するとする。
このとき、(53) の左辺を
までは (53) が成立するとする。
このとき、(53) の左辺を 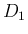 とし、
分子を 2 つに分けて
とし、
分子を 2 つに分けて
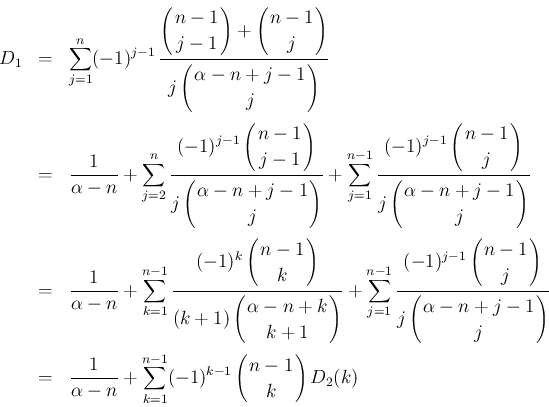
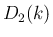 は、
は、
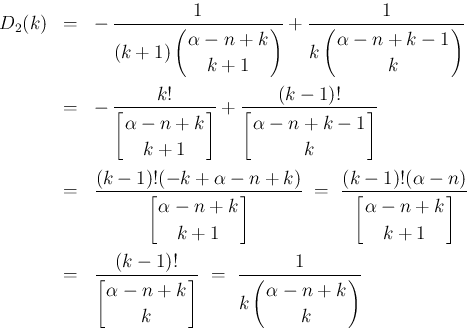
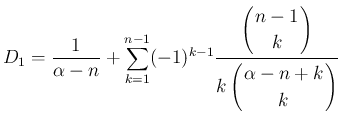
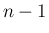 の式に等しいので、
帰納法の仮定により、
の式に等しいので、
帰納法の仮定により、
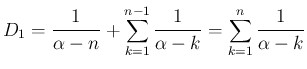
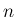 のときにも (53) が成り立つ。
のときにも (53) が成り立つ。
この補題 5 により、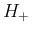 の
の
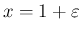 に関する
展開式 (51) は結局以下のようになる。
に関する
展開式 (51) は結局以下のようになる。
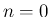 の式も
含んでいることに注意する。
の式も
含んでいることに注意する。
竹野茂治@新潟工科大学