3 エントロピー
保存則方程式の弱解は一意ではないため、
通常その解がエントロピー条件と呼ばれる物理的な条件を満たすことが要請される。
そこに現れる「エントロピー」とは、
いわゆる物理的なエントロピーを拡張した「一般化エントロピー」と
呼ばれるもの (数学的な実体) であり、
この一般化エントロピーは、一意解の選別の目安となるだけではなく、
補償コンパクト法で中心的な役割を持つ。
一般の 1 次元の保存則方程式
![\begin{displaymath}
U_t+F(U)_x=0\hspace{1zw}
\left(U=U(t,x)=\left[\begin{array...
...y}{c}f_1(U) f_2(U) \ldots f_N(U)\end{array}\right]\right)\end{displaymath}](img73.gif) |
(9) |
に対して、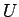 のスカラー値関数の組
のスカラー値関数の組
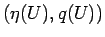 が (一般化) エントロピー対 であるとは、
が (一般化) エントロピー対 であるとは、
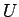 に関する連立線形微分方程式
に関する連立線形微分方程式
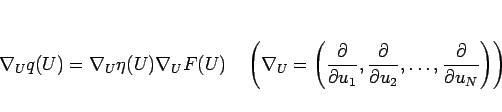 |
(10) |
を満たすことを言う。
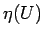 を エントロピー、
を エントロピー、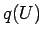 を エントロピー流束 と呼ぶ。
を エントロピー流束 と呼ぶ。
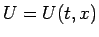 が (9) の滑らかな解であれば、
(10) より
が (9) の滑らかな解であれば、
(10) より
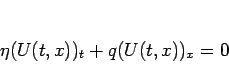 |
(11) |
という追加保存則が成り立つことになる。
保存則方程式の弱解 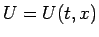 (
(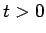 ,
, 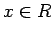 ) が満たすべき エントロピー条件 とは、
任意の、凸なエントロピーを持つエントロピー対
) が満たすべき エントロピー条件 とは、
任意の、凸なエントロピーを持つエントロピー対
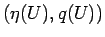 に対して、
超関数の意味で
に対して、
超関数の意味で
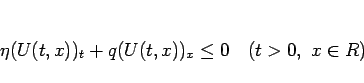 |
(12) |
を満たすこと、すなわち任意の非負な
![$\phi(t,x)\in C_0^1(]0,\infty[\times R)$](img81.gif) に対し、
に対し、
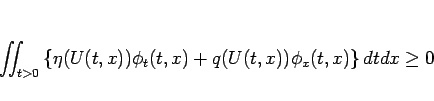
を満たすことである。このエントロピー条件を満たす弱解を エントロピー解 と呼ぶことがある。
実際には、物理的なエントロピーは凸ではなく逆に凹な関数で
総エントロピーは増大する (熱力学の第二法則) ので、
(12) とは符号が逆になる。
つまり一般化エントロピーは物理的なエントロピー 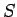 を
を 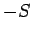 として含んでいることに注意する。
として含んでいることに注意する。
なお、1 節で紹介した Glimm の差分法や補償コンパクト法による弱解はいずれもエントロピー解であるが、
(3), (4) のエントロピー解が一意的であることは、
Glimm の差分法のように変動の十分小さい解については保証されているが、
補償コンパクト法による大きな初期値に対するエントロピー解については
まだその一意性は証明されていない。
保存則方程式 (9) が 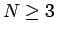 の場合、
方程式 (10) は 2 つの未知関数
の場合、
方程式 (10) は 2 つの未知関数 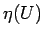 ,
, 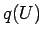 に対する
に対する 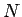 本の連立方程式、
すなわち過剰決定系なのでエントロピー対の存在は一般には保証されない。
逆に
本の連立方程式、
すなわち過剰決定系なのでエントロピー対の存在は一般には保証されない。
逆に 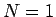 のとき、すなわち単独保存則方程式の場合は
方程式 (10) は 1 本なので、
任意の関数
のとき、すなわち単独保存則方程式の場合は
方程式 (10) は 1 本なので、
任意の関数 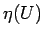 に対して (10) を満たす
に対して (10) を満たす 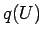 が取れる。
よって単独の方程式の場合には、ここから得られる豊富なエントロピー群を用いて Tartar 方程式を容易に解くことができる ([13] 参照)。
が取れる。
よって単独の方程式の場合には、ここから得られる豊富なエントロピー群を用いて Tartar 方程式を容易に解くことができる ([13] 参照)。
本稿で考察する 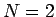 の場合は、(10) は 2 未知関数に対する 2 本の連立方程式なので、
エントロピーは存在するが初期条件の自由度程度にしか存在せず、
さらに
の場合は、(10) は 2 未知関数に対する 2 本の連立方程式なので、
エントロピーは存在するが初期条件の自由度程度にしか存在せず、
さらに 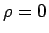 も含むような解を考察する場合は、
その初期条件も一つは固定されてしまいさらにエントロピーの自由度は減る。
本節では、そこで中心的な役割を果たすエントロピー対を与える公式や、
具体的なエントロピー対を紹介する。
も含むような解を考察する場合は、
その初期条件も一つは固定されてしまいさらにエントロピーの自由度は減る。
本節では、そこで中心的な役割を果たすエントロピー対を与える公式や、
具体的なエントロピー対を紹介する。
(10) は、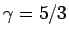 の方程式 (1) に対しては、2 節により
の方程式 (1) に対しては、2 節により
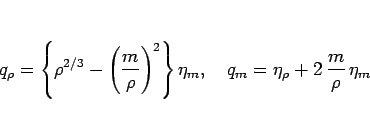
となるが、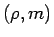 の代わりに
の代わりに 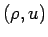 で考えれば (6) より、
で考えれば (6) より、
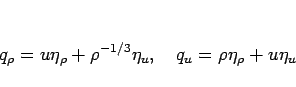
Riemann 不変量
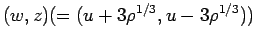 で考えれば (8) より、
で考えれば (8) より、
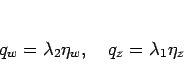 |
(13) |
となる。(13) から 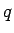 を消去すると、
いわゆる Euler-Darboux-Poisson の方程式
を消去すると、
いわゆる Euler-Darboux-Poisson の方程式
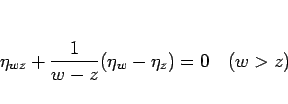
が得られる。
この 2 階線形微分方程式は Riemann 関数を用いて解くことができ、
特に 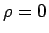 上 0 となる、いわゆる 弱エントロピー
上 0 となる、いわゆる 弱エントロピー
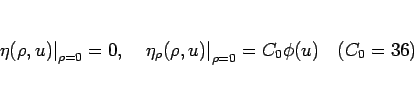
は、次の Darboux の公式
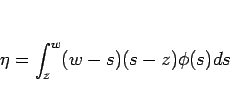 |
(14) |
で与えられる。この (14) のエントロピーに対するエントロピー流束 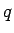 は、
は、
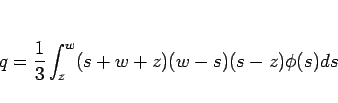 |
(15) |
で与えられる。
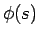 を与えることで (14), (15) によりエントロピー対 (外エントロピー) が得られることになる。
以下、本稿で重要なエントロピー対をいくつか紹介する。
を与えることで (14), (15) によりエントロピー対 (外エントロピー) が得られることになる。
以下、本稿で重要なエントロピー対をいくつか紹介する。
-
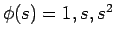
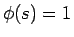 のとき、(14), (15) より
のとき、(14), (15) より
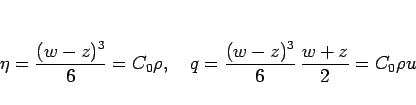
すなわちこれは密度と密度流束 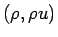 の定数倍であり、
この場合は (11) は質量保存則そのものとなる。
の定数倍であり、
この場合は (11) は質量保存則そのものとなる。
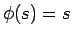 のときは、
のときは、
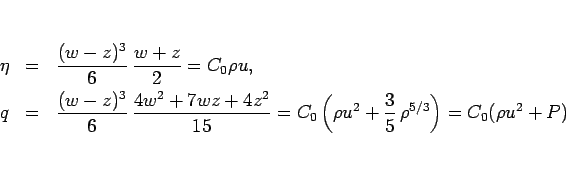
すなわちこれは運動量と運動量流束
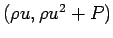 の定数倍で、
(11) は運動量保存則となる。
の定数倍で、
(11) は運動量保存則となる。
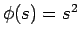 のときは、
のときは、
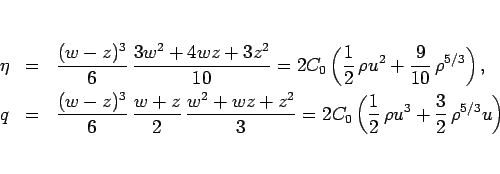
より、これは力学的エネルギーとエネルギー流束の対
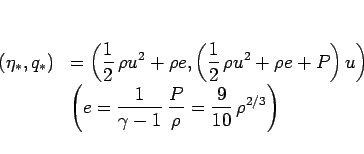
の定数倍になっていて、
この場合 (11) はエネルギー保存則となる。
-
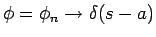
![$\phi_0(y)\in C_0^\infty(]0,1[)$](img110.gif) を
を
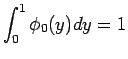 なるものとし、定数
なるものとし、定数 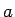 に対し
に対し
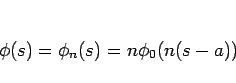 |
(16) |
とする。このとき
![$\mathop{\mathrm{supp}}\nolimits \phi_n(s)\subset [a,a+1/n]$](img113.gif) なので、
なので、
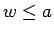 , または
, または 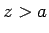 ならば、十分大きい
ならば、十分大きい 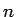 に対し
に対し
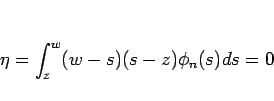
となる。
一方、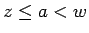 ならば十分大きい
ならば十分大きい 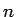 に対し
に対し
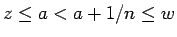 となるので、
となるので、
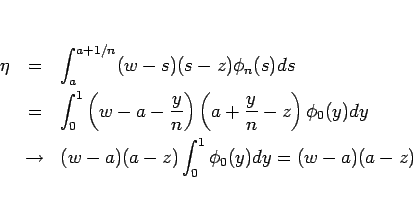
となる。よってこの極限は、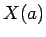 を
を
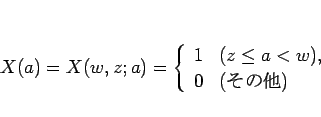
とすると
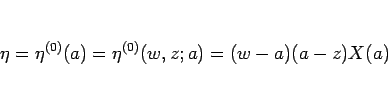
と書ける。これらは丁度 Darboux の公式 (14) の Riemann 関数を、
積分変数 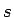 をパラメータ
をパラメータ 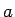 に替えて取り出したものになっている (内エントロピー)。
に替えて取り出したものになっている (内エントロピー)。
同様にこの 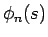 に対する
に対する 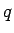 の極限は
の極限は
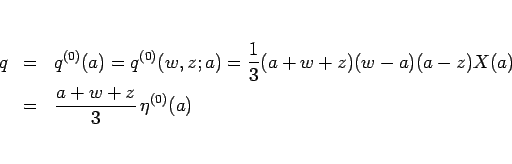
となる。
このエントロピー対は  、
、 で滑らかさが失なわれるが、
ほとんど至るところ (13) を満たす。
で滑らかさが失なわれるが、
ほとんど至るところ (13) を満たす。
なお、後で 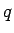 の代わりに
の代わりに
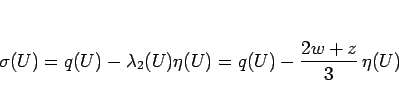
を用いることも多いが、この
 に対しては、
に対しては、
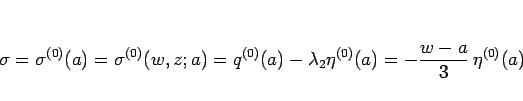 |
(17) |
となる。
同様に、
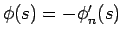 としたものの極限を考えると、部分積分により
としたものの極限を考えると、部分積分により
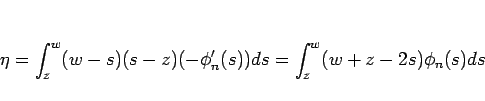 |
(18) |
となるので、
その極限は
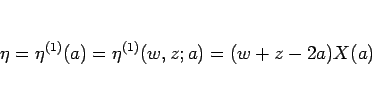
となる。同様に 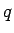 は
は
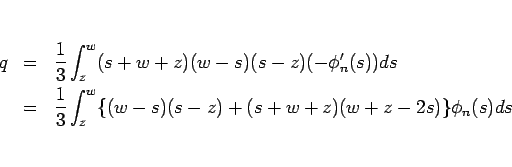
となり、よって  に対応する
に対応する  は、
は、
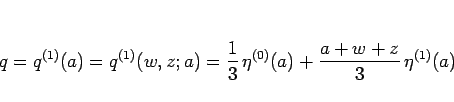
と書ける。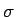 で書くと
で書くと
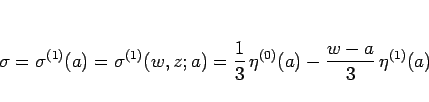
となる。なお、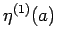 ,
, 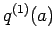 は、
は、
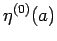 ,
, 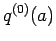 を
を 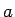 で微分したようなものになっていることに注意する。
で微分したようなものになっていることに注意する。
-
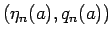 ,
,
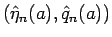
Tartar 方程式を解くのに重要なエントロピー対を紹介する。
それは、ある
![\begin{displaymath}
\psi_0(y),\hat{\psi}_0(y)\in C_0^\infty(]0,1[)
\end{displaymath}](img147.gif)
に対し、
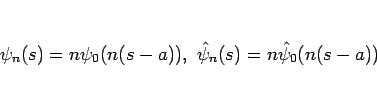
とおき、 としてこれらの 2 階微分
としてこれらの 2 階微分
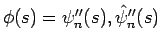 を取ったものに対する
エントロピー対であり、それらを
を取ったものに対する
エントロピー対であり、それらを
のように書くこととする。
部分積分により、
![\begin{eqnarray*}\eta_n
&=&
\int_z^w(w-s)(s-z)\psi_n''(s)ds
=
-\int_z^w(w+z-...
... &=&
-\left[(w+z-2s)\psi_n(s)\right]_z^w-\int_z^w 2\psi_n(s)ds
\end{eqnarray*}](img156.gif)
となるので、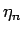 は
は
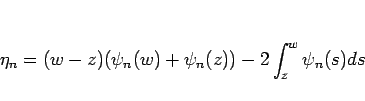 |
(21) |
と表される。同様に 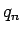 は、
は、
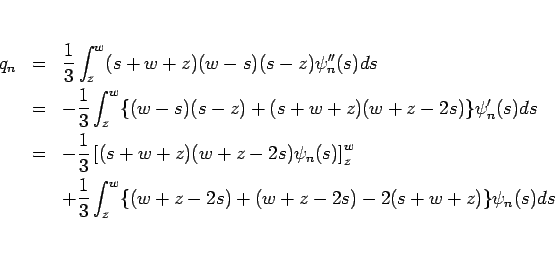
より、
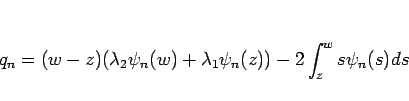 |
(22) |
となる。
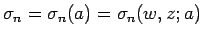 は、
は、
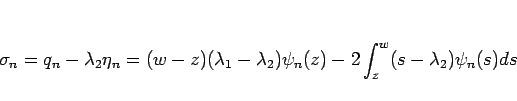
より、
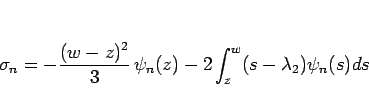 |
(23) |
となる。
もちろん、(21), (22), (23) の 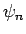 を
を 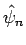 に変えたものがそれぞれ
に変えたものがそれぞれ 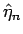 ,
, 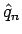 ,
,
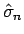 となる。
となる。
竹野茂治@新潟工科大学
2010年1月6日
![\begin{displaymath}
U_t+F(U)_x=0\hspace{1zw}
\left(U=U(t,x)=\left[\begin{array...
...y}{c}f_1(U) f_2(U) \ldots f_N(U)\end{array}\right]\right)\end{displaymath}](img73.gif)
![]() (
(![]() ,
, ![]() ) が満たすべき エントロピー条件 とは、
任意の、凸なエントロピーを持つエントロピー対
) が満たすべき エントロピー条件 とは、
任意の、凸なエントロピーを持つエントロピー対
![]() に対して、
超関数の意味で
に対して、
超関数の意味で
![]() を
を ![]() として含んでいることに注意する。
として含んでいることに注意する。
![]() の場合、
方程式 (10) は 2 つの未知関数
の場合、
方程式 (10) は 2 つの未知関数 ![]() ,
, ![]() に対する
に対する ![]() 本の連立方程式、
すなわち過剰決定系なのでエントロピー対の存在は一般には保証されない。
逆に
本の連立方程式、
すなわち過剰決定系なのでエントロピー対の存在は一般には保証されない。
逆に ![]() のとき、すなわち単独保存則方程式の場合は
方程式 (10) は 1 本なので、
任意の関数
のとき、すなわち単独保存則方程式の場合は
方程式 (10) は 1 本なので、
任意の関数 ![]() に対して (10) を満たす
に対して (10) を満たす ![]() が取れる。
よって単独の方程式の場合には、ここから得られる豊富なエントロピー群を用いて Tartar 方程式を容易に解くことができる ([13] 参照)。
が取れる。
よって単独の方程式の場合には、ここから得られる豊富なエントロピー群を用いて Tartar 方程式を容易に解くことができる ([13] 参照)。
![]() の場合は、(10) は 2 未知関数に対する 2 本の連立方程式なので、
エントロピーは存在するが初期条件の自由度程度にしか存在せず、
さらに
の場合は、(10) は 2 未知関数に対する 2 本の連立方程式なので、
エントロピーは存在するが初期条件の自由度程度にしか存在せず、
さらに ![]() も含むような解を考察する場合は、
その初期条件も一つは固定されてしまいさらにエントロピーの自由度は減る。
本節では、そこで中心的な役割を果たすエントロピー対を与える公式や、
具体的なエントロピー対を紹介する。
も含むような解を考察する場合は、
その初期条件も一つは固定されてしまいさらにエントロピーの自由度は減る。
本節では、そこで中心的な役割を果たすエントロピー対を与える公式や、
具体的なエントロピー対を紹介する。
![]() を与えることで (14), (15) によりエントロピー対 (外エントロピー) が得られることになる。
以下、本稿で重要なエントロピー対をいくつか紹介する。
を与えることで (14), (15) によりエントロピー対 (外エントロピー) が得られることになる。
以下、本稿で重要なエントロピー対をいくつか紹介する。
![]() のときは、
のときは、
![]() のときは、
のときは、
![]() を
を
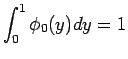 なるものとし、定数
なるものとし、定数 ![]() に対し
に対し
![]() に対する
に対する ![]() の極限は
の極限は
![]() の代わりに
の代わりに
![]() としたものの極限を考えると、部分積分により
としたものの極限を考えると、部分積分により