3.2
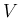 の評価: accurate method の場合
の評価: accurate method の場合
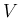 の評価: accurate method の場合
の評価: accurate method の場合
 と
と 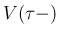 とは、
この
とは、
この 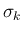 ,
, 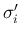 ,
, 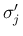 以外の front は共通なので、
となることがわかる。
この評価を、
以外の front は共通なので、
となることがわかる。
この評価を、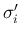 ,
,  の状況で場合分けして考える。
まずは、[A-1]、すなわち
の状況で場合分けして考える。
まずは、[A-1]、すなわち 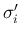 ,
,  が物理 front (膨張 front, 衝撃 front, 接触不連続 front) で、
が物理 front (膨張 front, 衝撃 front, 接触不連続 front) で、
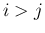 で、
で、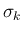 がその Riemann 問題の解から accurate method (p129-130) で作られた場合を考える。
この場合、当然
がその Riemann 問題の解から accurate method (p129-130) で作られた場合を考える。
この場合、当然
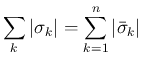
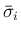 と
と
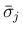 は
は 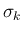 でも分解されていない。
Lemma 7.2 (i) より (1) の右辺は、
でも分解されていない。
Lemma 7.2 (i) より (1) の右辺は、
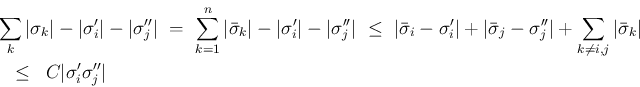
次に、[A-2]、すなわち accurate method で  の場合は、
Lemma 7.2 (ii) より
の場合は、
Lemma 7.2 (ii) より

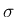 は十分小さい状況を考えているので、
Lemma 7.2 (ii) の
は十分小さい状況を考えているので、
Lemma 7.2 (ii) の
 の部分は
の部分は 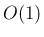 と
見ることができる。
と
見ることができる。
竹野茂治@新潟工科大学