3.3
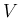 の評価: simplified method の場合
の評価: simplified method の場合
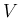 の評価: simplified method の場合
の評価: simplified method の場合
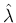 の非物理 front を
以後
の非物理 front を
以後 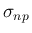 のように書くことにするが、
p125 一番下、あるいは p136 (7.52) にあるように、
その大きさは両側の定数解の差の絶対値と定義されていて、
各非物理 front 毎に違うものなので、
必要があれば
のように書くことにするが、
p125 一番下、あるいは p136 (7.52) にあるように、
その大きさは両側の定数解の差の絶対値と定義されていて、
各非物理 front 毎に違うものなので、
必要があれば  ,
, 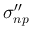 などの区別をする。
などの区別をする。
まずは、[S-1]、すなわち 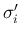 ,
,  が物理 front で
が物理 front で 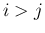 の場合 (p131 Figure 7.7)。この場合は、
の場合 (p131 Figure 7.7)。この場合は、
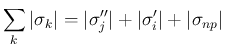
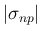 に等しく、
よって、Lemma 7.2 (iii) により、
に等しく、
よって、Lemma 7.2 (iii) により、

[S-2] の  の場合 (p131 Figure 7.8) も、
の場合 (p131 Figure 7.8) も、
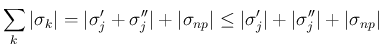
最後に、[S-3] の 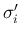 が非物理 front
が非物理 front 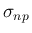 である場合
は (p131 Figure 7.9)、
である場合
は (p131 Figure 7.9)、
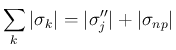
 (
(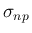 は
は  の
非物理 front、
の
非物理 front、
 は
は  の非物理 front) となり、
よって Lemma 7.2 (iv) により、(1) の右辺は
の非物理 front) となり、
よって Lemma 7.2 (iv) により、(1) の右辺は

これですべての場合に (7.55) が成り立つことが示された。
竹野茂治@新潟工科大学