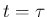
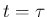 における
における 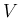 ,
, 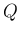 の差分評価である (7.55), (7.56) (p137)、
および帰納法による (7.60) (p138) の評価について考える。
の差分評価である (7.55), (7.56) (p137)、
および帰納法による (7.60) (p138) の評価について考える。
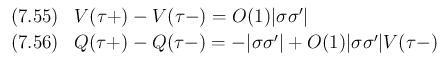
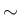 (7.34) から
得られると書いて、その下に 10 行程の説明があるが、
特にこの (7.56) の方は簡単ではないと感じたので、
本節でその詳細な証明を与えておく。
(7.34) から
得られると書いて、その下に 10 行程の説明があるが、
特にこの (7.56) の方は簡単ではないと感じたので、
本節でその詳細な証明を与えておく。
なお、特に  の場合の (7.56) の説明用に、
p137 に
の場合の (7.56) の説明用に、
p137 に  と
と 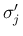 の front が
の front が 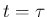 で
衝突して
で
衝突して 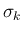 (
(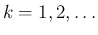 ) の front が発生するような図が
書いてあり本節でもそのような状況を考えるが、少し記号を変える。
左からの
) の front が発生するような図が
書いてあり本節でもそのような状況を考えるが、少し記号を変える。
左からの 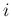 -特性族の front
-特性族の front 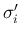 の方はそのままとするが、
右からの
の方はそのままとするが、
右からの  -特性族の front は
-特性族の front は  と書くことにして、
と書くことにして、
 の場合も同じ記号のまま議論できるようにする。
の場合も同じ記号のまま議論できるようにする。
生成する front は 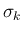 (
(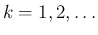 ) とするが、
この添字の
) とするが、
この添字の 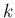 は「
は「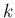 -特性族」を意味はせず
単純に左から順番に番号を振ったもので、
accurate method の場合の膨張波を分解する前の Riemann 問題の解の波は
-特性族」を意味はせず
単純に左から順番に番号を振ったもので、
accurate method の場合の膨張波を分解する前の Riemann 問題の解の波は
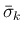 (
(
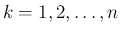 ) と書くことにする。
この場合、
) と書くことにする。
この場合、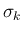 は、この
は、この
 の
うち、膨張波を分解 front に分離して作成した front の集まり (の速度を微小に変更したかもしれないもの) となる。
この場合、Lemma 7.2 (i),(ii) の評価は、
の
うち、膨張波を分解 front に分離して作成した front の集まり (の速度を微小に変更したかもしれないもの) となる。
この場合、Lemma 7.2 (i),(ii) の評価は、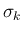 ではなく、
ではなく、
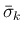 に対して成り立つものであることに注意する。
に対して成り立つものであることに注意する。
以下、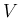 ,
, 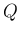 の評価を、順に衝突点での近似解の作り方に関する場合分けで
示すことにするが、そのそれぞれに以下のように名前をつけておくことにする。
の評価を、順に衝突点での近似解の作り方に関する場合分けで
示すことにするが、そのそれぞれに以下のように名前をつけておくことにする。
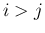 の場合
(異なる特性族の流入 front の衝突)
の場合
(異なる特性族の流入 front の衝突)
 の場合
(同じ特性族の流入 front の衝突)
の場合
(同じ特性族の流入 front の衝突)
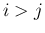 の場合
の場合
 の場合
の場合
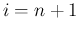 )
)
なお、等式形の (7.55), (7.56) を示すことは難しく (成り立たないかもしれない)、
かつそれは必要はなく、実際に必要で示すべきは不等式形の
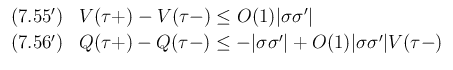
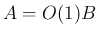 は、ある定数
は、ある定数 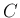 に対し
に対し
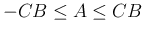 ,
すなわち
,
すなわち 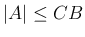 を意味し、つまり
を意味し、つまり 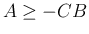 も必要であるが、
も必要であるが、
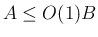 は
は 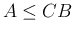 のみを意味するので、
(7.55), (7.56) を示すためには、正確には下からの評価も必要であるが、
実際には下からの評価は必要ないし、簡単に示すこともできない。
実際、[1] のこの部分に関する原論文である [2] にも 等式形の (7.55), (7.56) ではなく、不等式形の (7.55'), (7.56') の形で
書いてある。
本稿も、(7.55), (7.56) ではなく、(7.55'), (7.56') を示すことを考える。
のみを意味するので、
(7.55), (7.56) を示すためには、正確には下からの評価も必要であるが、
実際には下からの評価は必要ないし、簡単に示すこともできない。
実際、[1] のこの部分に関する原論文である [2] にも 等式形の (7.55), (7.56) ではなく、不等式形の (7.55'), (7.56') の形で
書いてある。
本稿も、(7.55), (7.56) ではなく、(7.55'), (7.56') を示すことを考える。
竹野茂治@新潟工科大学