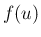 を折れ線近似 (polygonal approximation) することで区分的に定数な近似解を構成している。
を折れ線近似 (polygonal approximation) することで区分的に定数な近似解を構成している。
波面追跡法は、大きく 2 通りの解の構成法があり、 その一つが本稿で取り上げた Bressan 流の方法で、 [1] が保存則方程式全般の話を含む解説書、 [2] がその波面追跡法の部分の原論文である。 もう一つの方法が、Risebro 流の方法で、 [5] が保存則方程式全般の話を含む解説書、 [4] がその波面追跡法の部分の原論文である。
本稿で取り上げた [1] (Bressan) の方法は、 原論文 [2] (Bressan) の方法に、 論文 [3] (Baiti-Jenssen) による改良を加えたもので、 原論文 [2] よりもだいぶ易しくなっている。
一方の Risebro 流の方法 [4] は、 [1] が導入している非物理 front や、世代番号は用いず、 また速度の変更も行わない形での評価を行うもので、 むしろ Bressan 流の説明よりもわかりやすいところもあるが、 逆に a priori 評価を得ること、 および近似解が無限に延長できることを示すことが難しくなっている。 実際、膨張波を不連続波で近似し、 すべての衝突で Riemann 問題を解いて同じことを進めようとすると、 front の数がどんどん増えてその衝突がとても多くなってしまって 有限時間でその構成が停止してしまう可能性があるが、 [4] では、あるところまでいったら小さい front を捨てることで その問題を解消しているようである。
[1] の行っている速度の変更も Risebro 流では行わないので、 3 つ以上の front の衝突も起こりうるが、 [5] (Holdel-Risebro) にはそのような評価も書かれている。 なお、[5] は、front 総数の評価のため、 世代番号も導入しているようなので、 [5] は原論文 [4] (Risebro) に [1] (Bressan)、 あるいは [2] (Bressan), [3] (Baiti-Jenssen) の改良を 追加したようなものなのかもしれないが、詳しくは読んでいない。
保存則方程式の最近の代表的な解説書としては、
古くからの第一人者による [7] (Defermos) が
有名であるが、これも波面追跡法を取り上げていて、
連立の保存則方程式に対しては Bressan 流の方法を解説し、
単独保存則方程式に関する波面追跡法については、
筆者による [6] を解説している。
なお、波面追跡法は元々 [6] から始まったと言ってよいらしいが、
単独保存則方程式では、膨張波を不連続波で近似するというよりも、
むしろ流束関数 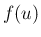 を折れ線近似 (polygonal approximation) することで区分的に定数な近似解を構成している。
を折れ線近似 (polygonal approximation) することで区分的に定数な近似解を構成している。
それに対し、それを連立保存則方程式で使えるようにしたのが [8] (DiPerna) などであるらしい。
[8] は、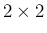 の連立保存則方程式に対して、
流束関数はいじらずに、
膨張波を非物理的衝撃波 (エントロピー条件を満たさない衝撃波) で
近似することで区分的に定数な近似解を構成しているようだが、
の連立保存則方程式に対して、
流束関数はいじらずに、
膨張波を非物理的衝撃波 (エントロピー条件を満たさない衝撃波) で
近似することで区分的に定数な近似解を構成しているようだが、
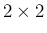 の場合は一般の
の場合は一般の 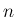 本の場合と違い、
色々いいところがあって、
front の総数が有限個でおさまることなどが
比較的容易に示されるそうである。
詳しくは読んでいない。
本の場合と違い、
色々いいところがあって、
front の総数が有限個でおさまることなどが
比較的容易に示されるそうである。
詳しくは読んでいない。
[9] (Jenssen) は、直接波面追跡法とは関係ないものの、
ある意味で波面追跡法の限界を示しているとも言える論文で、
特殊な 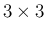 の連立保存則方程式で、
大きな初期値に対しては、区分的に定数な解 (近似解ではなく厳密解) が
有限時間で爆発する、すなわち解の
の連立保存則方程式で、
大きな初期値に対しては、区分的に定数な解 (近似解ではなく厳密解) が
有限時間で爆発する、すなわち解の 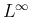 ノルムが無限大に発散したり、
全変動が無限大に発散する例を具体的に構成している。
この論文の概要には、それらに関する色々な論文が詳しく紹介されていて、
それを読むだけでもだいぶ勉強になる。
このような波面追跡法の限界に関する研究は他にもいくつかあるらしいが、
あまり詳しくは知らない。
ノルムが無限大に発散したり、
全変動が無限大に発散する例を具体的に構成している。
この論文の概要には、それらに関する色々な論文が詳しく紹介されていて、
それを読むだけでもだいぶ勉強になる。
このような波面追跡法の限界に関する研究は他にもいくつかあるらしいが、
あまり詳しくは知らない。
ほかに 3 編ほど日本人によるものをあげる。
[10], [11] (浅倉) は、この分野の日本での第一人者による
解説記事で、
[10] は Glimm 差分と Bressan 理論などの紹介記事であり、
波面追跡法の紹介は少ないが Bressan 理論全体を見通すにはよく、
[11] は、少し丁寧に波面追跡法と補完速度法 (補償コンパクト性理論) に
ついて説明している。
説明は、基本的には Bressan 流だが、
front 速度の変更を行わずに沢山の front の同時衝突を
考慮しているところは Holden-Risebro 流の評価を利用し、
世代番号評価も用いる、という方法をとっている。
そのような流れの説明が一番わかりやすいのかもしれない。
[12] (應和) は、この分野のあらたな日本の研究者による論文で、
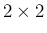 の連立方程式の場合に [1] の手法を大幅に
改善する方法を論じている。
の連立方程式の場合に [1] の手法を大幅に
改善する方法を論じている。
なお、今回これをまとめるにあたって、 ほぼ一から波面追跡法を [1] に沿って読み直したのであるが、 波面追跡法の勉強はこれで 4 回目位になる。 一番最初に勉強したのは 20 年以上前であったが、 しかし、勉強し直すたびに、 前回の理解、前回のノートににあまいところがあったと 反省しているような気がする。 つまり、波面追跡法は、[1], [5] などによりだいぶ 整備されてきているとはいえ、 どの方法であっても、わかりにくいところ、 落し穴のようなところがあり、 だれもが容易にわかるようにはまだ整理されていない理論であると言えるだろうし、 今後のさらなる改良が待たれる理論なのだろうと思う。
そして、このノートも私のまた間違った理解が含まれている可能性が十分にある。 そのようなものに気がついたら、是非ご一方頂ければと思う。
また、本来のいわゆる「Bressan 理論」とは、本稿の内容の続きの話、 すなわち [1] の 8 章以降の半群の生成や一意性などの話こそが 重要なのであるが、私はまだそちらには手を出していない。 機会があればそちらも勉強してみたいが、 多分だいぶ先のことになるだろう。
竹野茂治@新潟工科大学