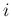
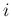 -,
-, -特性族に出る front の世代はそれぞれ
-特性族に出る front の世代はそれぞれ 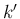 ,
, 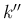 のままで、
(52) よりそれ以外の特性族に出る front の
世代は
のままで、
(52) よりそれ以外の特性族に出る front の
世代は 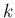 以上となる。
よって
以上となる。
よって
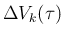 は、
は、

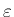 ,
, 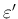 は 0 または 1)。
よっていずれにしても
で評価され、
Lemma 7.2 (i) より (53) の 1 本目が得られる。
は 0 または 1)。
よっていずれにしても
で評価され、
Lemma 7.2 (i) より (53) の 1 本目が得られる。
同様に
 は、
は、
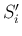 は
は
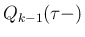 に含まれる
に含まれる 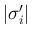 の係数、
の係数、
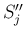 は
は
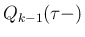 に含まれる
に含まれる 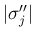 の係数で、
もし
の係数で、
もし 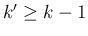 なら
なら
 となるが、
となるが、
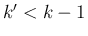 なら
なら
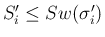 であり、
であり、
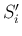 は
は 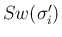 のうち
のうち 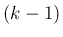 以上の世代の項のみの和となる。
以上の世代の項のみの和となる。
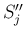 も同様。
も同様。
いずれにせよ、
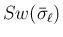 ,
,
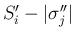 ,
,
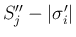 は
は 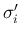 ,
,  ,
,
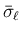 を
含まず、よって
を
含まず、よって 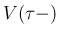 に含まれるので、
に含まれるので、

竹野茂治@新潟工科大学