最新の開発版 (git) の all.dem の出力を置いておきます。
- all.dem の PDF 出力 (2023-11-28 の GIT 版)
all-current-20231129.pdf (783 ページ、26,582,803 Byte) - その画像を小さくした一覧 (2023-11-28 の GIT 版)
all-20231129-list.pdf (14 ページ、34,446,581 Byte)
「情報やメモ (09/29 2023)」 の時点でのデモ (782 ページ) に比べると、1 ページ分だけ増えていますが、 これは、polygon_border.dem の分の追加 (762 ページ) です。
この間の改変には以下のようなものがあります (以下以外にも色々あると思いますが最近は変更全体を把握していません)。
- 新規コマンド warn "message" の追加
- multiplot モードに関する replot の改善 (remultiplot)
- plot with polygons (= plot with filledcurves closed) で最初の点と最後の点が一致していない場合もサポート
- unset pointintervalbox
- 疑似ファイル '+' の個別のグラフの範囲指定用に、 sample キーワード以外に空の標本増分を指定できるように
- keyentry で文字列を凡例の位置にも書けるように
1. は、printerr 同様にメッセージを常に stderr に出力するコマンドですが、 指定メッセージの出力前に、現在のファイル名 (か関数ブロック名)、 および現在の行番号を追加して出力します。デバッグ用により便利です。
2. は、従来の multiplot では、replot がうまく効かずに、 multiplot 内の最後の plot のみ replot し、 それ以外のものは破壊していました。 今回の新しい機能では、最後の multiplot で実行したコマンドをすべて データブロック $GPVAL_LAST_MULTIPLOT に記録し、 それを remultiplot で実行できるようになりました。 replot でも、直前のコマンドが multiplot の一部であれば自動的に remultiplot を呼び出してくれますし、 mouse 操作による zoom/pan などの際の再描画でも remultiplot が呼び出されるようになります (set mouse multiplot 時には)。 ただし、完全というわけではないようですし、 マウス操作の対応も、例えば mouse による座標の取得は、 最後の plot に関する軸での計算になってしまうようです。
3. は、多分上に書いたデモの追加部分だと思います。
4. は、例えば linespoints に関する話で、 従来は linespoints は線 (lines) を書き、 点記号の下を消してから点記号 (points) を書いていた、 すなわち「不透明」な点記号を描画していました。 その「消す」部分のサイズの指定が set pointintervalbox だったわけですが、 今回「unset pointintervalbox」を使うことで、 点記号部分を消さずに点記号が書けるようになりました。 これにより「透明」な点記号を使えるようになったことになります。 なお、これは linespoints だけではなく、 xerrorbars, xyerrorbars などの誤差線にも適用されます。
5. は、plot コマンド上で指定する軸の範囲指定と、 サンプリング範囲指定の区別がやや曖昧だったために、 これまでは必要なら sample キーワードを追加する、 という仕様だったものを、サンプリング範囲指定には 3 番目のフィールドとしてサンプリング間隔を指定できるようにして、 そこを空欄にすれば、サンプリング範囲指定と軸の範囲指定の区別ができる、 という効果を狙ったもののようです。例えば、
set xrange [0:50]
plot [0:10] f(x), [10:20] g(x), [20:30] h(x)
set xrange [0:50]
plot sample [0:10] f(x), [10:20] g(x), [20:30] h(x)
set xrange [0:50]
plot [0:10:] f(x), [10:20] g(x), [20:30] h(x)
6. は、例えば「keyentry "文字列" left」などとすれば、 key の通常なら凡例を置く場所に左合わせで文字列が書かれる、 というもので、それにより key の幅全体に渡る文字列を置けるようになる、 というものです。
なお、4., 5., 6. などは、 今までもできていたのかどうかは確認していませんので、 もしかしたら新たな機能というわけではなく、 単に今回新たにドキュメント化したというだけなのかもしれません。
(cf. 「情報やメモ (08/23 2024)」)
今さら珍しくない話ですが、数列をグラフ化する方法について紹介します。 数列データがデータファイルとして存在する場合は、 単に with lp でグラフ化することができますが、 それを、一般項、あるいは漸化式から、ファイルを経由せずに gnuplot でグラフ化する、という方法について考えます。
それは現在の gnuplot では少しも難しくなく、以下により簡単にできます。
- 疑似ファイル '+' を利用する
- plot sample を利用する
例として、
π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...のグラフを書いてみます。
- コード:
f(n) = sum [j=1:n] (-1)**(j-1)/(2*j - 1.0)
N = 20
set xrange [0.5:N+0.5]
set yrange [0.6:1.1]
set grid
set sample N
plot sample [n=1:N] '+' using (n):(f(int(n))) with lp title "部分和のグラフ", pi/4.0 - そのグラフ
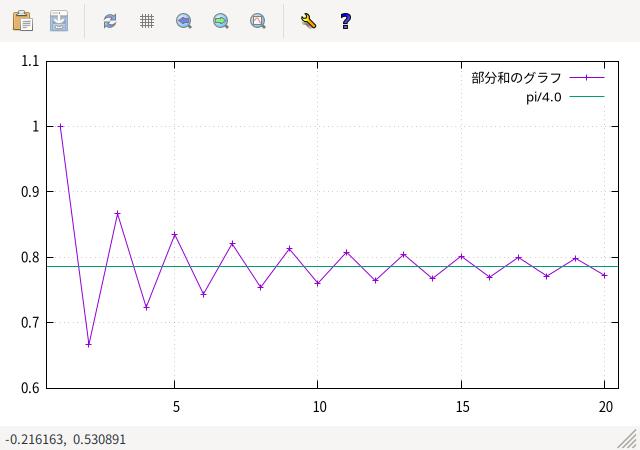
最初の f(n) は、第 n 部分和の定義です。 f(1) から f(N) までを、(x,y)=(n,f(n)) の点を折れ線でつないだグラフにします。
疑似ファイル '+' は、xrange と set sample の数字によって x の標本点を作成します。しかし、グラフの枠線と重ならないように xrange を上のように少し広げる場合は、 plot の sample キーワードを使って実際にサンプルする範囲と 変数を指定すればできます。
なお、f(n) ではなく f(int(n)) としていますが、 サンプル値は一般には実数になるので、int(n) としないと sum でエラーがでます。
一般項ではなく漸化式の場合は、plot の行を例えば
yy = 0
plot sample [n=1:N] '+' using (n):(yy = yy+(-1)**(n-1)/(2*n-1)) with lp
title "部分和のグラフ", pi/4.0
最新の開発版 (git) の all.dem の出力を置いておきます。
- all.dem の PDF 出力 (2023-09-26 の GIT 版)
all-current-20230929.pdf (782 ページ、26,581,502 Byte) - その画像を小さくした一覧 (2023-09-29 の GIT 版)
all-20230929-list.pdf (14 ページ、34,350,678 Byte)
「情報やメモ (08/29 2023)」 の時点でのデモ (776 ページ) に比べると、6 ページ分だけ増えていますが、 これは、新たに追加された hstep スタイル用のデモの追加分です。
- demo/hsteps.dem, demo/hsteps_histogram.dem, demo/rank_sequence.dem, demo/logic_timing.dem の分の追加 (353-358 ページ)
この間の改変としては、 なんといっても上に書いた描画スタイル with hsteps の追加でしょう。 作成したのは、最近活発に開発チームで関わっている Hiroki Motoyoshi さんです。 以前の開発 with sectors と同様に、色々なサンプルが追加されています。
実は、以前 「情報やメモ (05/09 2023)」 などに書いたヒストグラムの「グループ毎の接続線」について、 描画スタイル histogram にそういうオプションを追加してもらえると、 という要望をだいぶ前に本家に出していたのですが、 つい最近、 histogram には実装していないけれど、 最近追加された hsteps を使うとそれができるようになったのでもういいよね、 という返事がきました。 今度試してみて、また報告したいと思います。
毎度おなじみ、レーダーチャートの件です。 「情報やメモ (04/06 2021)」, 「情報やメモ (09/23 2022)」 で、spiderplot によるレーダーチャートの作成例を紹介しました。
実は私のところでは、そこで紹介したような複数人 (3 人) のレーダーチャートを重ねて描く、 すなわち人数分のレーダーチャートの重ね描きからなるグラフ 1 つを 作成するのに利用しているのではなく、 むしろ主に各人毎のレーダーチャートを平均と重ねて描く、 すなわち 2 つのレーダーチャートのグラフを人数分作成する、 という形で利用しています。今回はその方法について紹介します。 またついでに、あらためて spiderplot で気がついたことについても紹介します。
データは今までと同じものを利用します。すなわち、data.dat が
生徒 国語 社会 理科 算数 英語であるとします。 そして、平均値と重ね描きするため、 あらかじめ平均値も別に計算しておき、そのファイルを mean.dat とします。
Aさん 70 80 60 50 90
Bさん 40 20 90 90 70
Cさん 90 90 90 90 90
平均 66.67 63.33 80.00 76.67 83.33
実は、spiderplot では、 この別々のファイルのデータを一つのグラフに重ね描きするために newspiderplot という命令があります。 それを利用して別々のファイルからデータを読んで重ね描きするか、 または 2 つのデータを連結して、
生徒 国語 社会 理科 算数 英語のようにしたデータ (comb.dat) からグラフを作成することも可能です。 表計算ソフトなどから出力したデータの場合は 後者の連結したデータを元にすることも多いと思います。 今回はその両者、すなわち
Aさん 70 80 60 50 90
Bさん 40 20 90 90 70
Cさん 90 90 90 90 90
平均 66.67 63.33 80.00 76.67 83.33
- [a-1] 別ファイル data.dat (人数 + 1 行), mean.dat (1 行) を利用する方法
- [a-2] 連結したファイル comb.dat (人数 + 2 行) を利用する方法
を紹介します。
また、データのヘッダにある科目名の情報は spiderplot の軸のラベルとして使いますが、 その取得の方法も複数のやり方が考えられます。ここでは、
- [b-1] title columnheader を利用する方法
- [b-2] ` ` (バッククォート) を使って自前で取得する方法
を紹介します。[b-1] は前の例で紹介した方法ですが、 [b-2] は Unix なら head コマンドで可能で、 MS-Windows なら gawk で代用できます。
さらにデータ 1 列目の生徒の名前の情報は key のラベルとして使用しますが、 その取得は
- [c-1] 配列と stats を利用する方法
- [c-2] key(1) を利用する方法
があります。[c-1] は前に紹介した方法です。
まずは複数グラフの出力についてですが、 PNG や SVG のような単体画像ファイルを生成する場合は、 「set output [ファイル名]」として plot して「set output」とする、 という作業が必要になりますが、 複数ページをサポートしている PDF ファイルや PostScript ファイルの場合は、 plot コマンドを複数回実行すれば、 それに応じて複数ページの出力ファイルが生成され、 各 plot は各ページに出力されます。ファイル指定は 1 つで良くなります。 どうせ do for 文で実行するので手間の違いはたいしたことではありませんが、 例えば pdfcairo terminal を利用すると便利です。
次は [a-1],[a-2] について考えます。 M を人数、N を科目数として (これらは stats で取得可能)、 [a-1] の場合は、基本的な plot 部分については、 以下のように plot します (サンプルは こちら (spider-multi-1.pdf))。
set spiderplot
set for [i=1:N] paxis i range [0:100]
do for [k=1:M] {
plot for [j=1:N] "mean.dat" using j+1 lt 1 lw 1,\
newspiderplot,\
for [j=1:N] "data.dat" using j+1
every ::k::k lt 2 lw 5
}
[a-2] の場合は、every を使って、 k+1 行目と M+2 行目を描画させるようにします (サンプルは こちら (spider-multi-2.pdf))。
set spiderplot
set for [i=1:N] paxis i range [0:100]
do for [k=1:M] {
plot for [j=1:N] "comb.dat" using j+1
every M-k+1::k lw 4
}
次は、[b-1],[b-2] について考えます。 spiderplot では plot の title は key に入るのではなく、 各軸のラベルになります。[b-1] はそれを columnheader で取得する方法で、 上の plot の例で言えば、data.dat か comb.dat の plot の最後に 「title columnhead」をつければいいです。 ただし、その場合 1 列目が通常のデータとは見なされなくなるので、 every 指定が 1 減ることになります。 例えば [a-1] で [b-1] を行う場合は以下の通りです (サンプルは こちら (spider-multi-3.pdf))。
set spiderplot
set for [i=1:N] paxis i range [0:100]
do for [k=1:M] {
plot for [j=1:N] "mean.dat" using j+1 lt 1 lw 1,\
newspiderplot,\
for [j=1:N] "data.dat" using j+1
every ::k-1::k-1 lt 2 lw 5 title columnheader
}
[b-2] の場合は、unix ならバッククォートを用いて
chead = "`head -1 data.dat`"
chead = "`gawk \"NR==1\" data.dat`"
chead = "`head -1 data.dat`"
set for [j=1:N] paxis j label word(chead, j + 1)
最後は [c-1],[c-2] ですが、[c-1] は前に紹介した通り、 stats によるデータファイルの空読みを利用して、 1 列目を配列に保存する方法です。 その配列の値は、plot の際に keyentry を使って key に利用できます (サンプルは こちら (spider-multi-5.pdf))。
array name[M]
j = 0
stats "data.dat" every ::1
using 2:(j = j + 1, name[j] = strcol(1), 0) noout
set spiderplot
set for [i=1:N] paxis i range [0:100]
set key box
do for [k=1:M] {
plot\
keyentry with l lt 1 lw 1 title "平均",\
keyentry with l lt 2 lw 5 title name[k],\
for [j=1:N] "mean.dat"
using j+1 lt 1 lw 1,\
newspiderplot,\
for [j=1:N] "data.dat" using j+1
every ::k-1::k-1 lt 2 lw 5 title columnheader
}
それに対して [c-2] は、配列は必要なく、plot の際に
「using j+1:key(1)」とする方法です。
これでもちゃんと 1 列目が key になります。
これだと、keyentry は不要になりますが、
key の凡例が with lines ではなく with box のようになります
(サンプルは こちら
(spider-multi-6.pdf))。
set spiderplot
set for [i=1:N] paxis i range [0:100]
set key box
do for [k=1:M] {
plot for [j=1:N] "mean.dat" using j+1:key(1)
lt 1 lw 1,\
newspiderplot,\
for [j=1:N] "data.dat" using j+1:key(1)
every ::k-1::k-1 lt 2 lw 5 title columnheader
}
あとは、 「情報やメモ (04/06 2021)」 のように paxis に tics を設定して、 set grid spider でその tics をつなぐ多角形を書いてやれば完成です。 [a-1],[b-1],[c-2] での例を以下に示します (サンプルは こちら (spider-multi-7.pdf))。
### M,N の取得
stats "data.dat" every ::1 using 2 noout
M = STATS_records
N = STATS_columns - 1
### teminal と出力ファイル
set term pdfcairo size 6,4
set output "spider-multi-7.pdf"
### グラフの設定
set spiderplot
set for [i=1:N] paxis i range [0:100]
set paxis 1 tics font ",9" # 刻みの数字は 1 番軸のみ
set grid spider lt 1 lc "gray" lw 0.5 back
set key box
### 描画
do for [k=1:M] {
plot for [j=1:N] "mean.dat" using j+1:key(1)
lt 1 lw 1,\
newspiderplot,\
for [j=1:N] "data.dat" using j+1:key(1)
every ::k-1::k-1 lt 2 lw 5
title columnheader
}
(cf. 「情報やメモ (04/10 2025)」)
最新の開発版 (git) の all.dem の出力を置いておきます。
- all.dem の PDF 出力 (2023-08-28 の GIT 版)
all-current-20230829.pdf (776 ページ、26,566,356 Byte) - その画像を小さくした一覧 (2023-08-29 の GIT 版)
all-20230829-list.pdf (13 ページ、34,143,541 Byte)
「情報やメモ (05/30 2023)」 の時点でのデモ (772 ページ) に比べると、4 ページ分だけ増えていますが、 これは前回報告した
- demo/contourfill.dem の分の追加 (420-423 ページ)
です。
この間 (2023-05-26 以降) の git 版の改変としては、 以下のようなものがあるようです。 なお、主にドキュメントの差分で見ているので、 変更はほかにもあると思います。
- set colorbox の cbtics オプションの削除
- qt6 のサポート
- set terminal kittycairo に transparent オプションを追加
(cf. 「情報やメモ (09/29 2023)」)
最近、LaTeX などのフォントの書体を変えて使ったりしているのですが、 フリーの TrueType フォントをたくさんダウンロードした際に、 どのような見た目のフォントか、太さはどうかなどを比較するために フォントの見本を作ろうと考えました。
古い freetype ライブラリにはそういった目的用の、 指定したフォントで文字列を書かせてみるツール (freetype 1 の頃の ftdump とか ftzoom とか) がついていましたが、 多くのフォントのものを見る場合はそれも手間です。
他に思いついたのは、freetype ライブラリを直接使うか libgd ライブラリを使って C でそういうプログラムを書くこと、 あるいは GD モジュールを使って perl でそういうプログラムを書くことでしたが、 よく考えたら、それは gnuplot でやらせるのと変わりませんし、 gnuplot でやるのが一番手軽だと気がつきました。 そこで、gnuplot でやってみました。
以下に示すのがその csh スクリプトで、gnuplot を呼び出して、 指定したディレクトリ内の TrueType フォント (*.ttf, *.ttc, *.otf, *.TTF, *.TTC) の見本を作成するものです。 ただし、gnuplot が libgd を使ってコンパイルされている必要がありますし、 fontconfig が有効な libgd の場合は、 フォントの絶対パスを指定しても 正しくそのフォントを使ってくれない可能性があります。 横がはみでたり、縦のサイズが適切でなかったりしたら、 pngH, yH, pngW などの数値を変えてみてください。
#! /bin/csh -f
set gnuplot = gnuplot
set png = outf.png
set fontd = /usr/local/share/fonts/aozoramincho
set fontlist = ( $fontd/*.{ttf,ttc,otf,TTF,TTC} )
set fnamelist = ( )
foreach i ( $fontlist )
set fnamelist = ( $fnamelist `basename $i` )
end
# 以下が gnuplot 実行部分
$gnuplot <<EOF
N = $#fnamelist # フォント数
pngH = 50 # 1 行分の png サイズでの高さ
pngW = 600 # png サイズでの出力ファイルの横幅
yH = 10 # グラフ座標での 1 行分の高さ
set term png size pngW,pngH*N
array Fname = split("$fnamelist")
set out "$png"
set xrange [0:100]
set yrange [0:yH*N]
str = "私のなまえは竹野茂治です。"
unset xtics
unset ytics
unset border
do for [j=1:N] {
set label j sprintf("%s%s", str, Fname[j])
at 0, yH*(N-j) \
font "${fontd}/".Fname[j].",20"
}
plot 1/0 not
set out
EOF
xli $png # xli は外部の画像ビューワプログラム
- 上の出力の画像ファイル:

unset xtics, unset ytics, unset border で グラフの枠や軸の刻みなど不要な要素を消して、 set label で文字列 (str + フォント名) を指定したフォントで表示させています。 フォント名は、最近導入された配列と split() を組み合わせて配列化していますが、 他のやり方もあるかもしれません。
gnuplot の本来の使い方ではないですが、 最近の do for や配列などの機能の充実により、 gnuplot でもこういうことが楽にできるようになってきました。
最新の開発版 (git) の all.dem の出力を置いておきます。
- all.dem の PDF 出力 (2023-05-26 の GIT 版)
all-current-20230529.pdf (772 ページ、26,384,531 Byte) - その画像を小さくした一覧 (2023-05-26 の GIT 版)
all-20230529-list.pdf (13 ページ、36,747,932 Byte)
「情報やメモ (04/07 2023)」 の時点でのデモ (771 ページ) に比べると、1 ページ分だけ増えていますが、
- pm3d.dem の 461 ページのものが 461, 462 ページの 2 つに
という形で、これは 「情報やメモ (05/24 2023)」 で紹介した 5.4.7 で行われた変更と同じものです。
この間 (2023-04-05 以降) の git 版の改変としては、 以下のようなものがあるようです。 なお、ドキュメントの差分で見ているので、 変更はほかにもあると思います。
- 描画スタイル with contourfill, set contourfill の新設
- 新しい出力形式 kittygd, kittycairo
- dumb, sixel, block, domterm などでの pause mouse 時の疑似マウス操作
- 関数ブロックを利用した新たな応用
1. は新しい描画スタイルで、 等高線の間を個別の色で塗り潰すことを可能にするもので、 demo に contourfill.dem が追加されています。 まだ本家の demo サイトには現れてはいないようです。
2. は kitty という端末エミュレータで実装されている kitty グラフィックプロトコルを使って、 それをサポートする端末エミュレータ上でグラフを表示するものです。 sixel グラフィックのようなものですが、 カラーがふんだんに使えるなど、sixel ドライバよりも優位性があるようです。 ただし、kitty プロトコルをサポートする端末エミュレータが どれくらいあるのかはよくは知りません。
3. も端末エミュレータ用の話で、それ用の出力形式で pause mouse 中に 矢印キーなどを使って視方向を変えたり (3 次元グラフ)、 視点移動や拡大 (2 次元グラフ) などが行えるようにするものです。
4. は、ドキュメントに追加されているのですが、 「これを使う以外には存在できないような状況でその実行を可能にする」 ためものだそうです。
例として、 2 つの CSV ファイルのグラフを同時に描画する際に、 一方はカンマ (,) 区切りの CSV ファイル、 もう一方はセミコロン (;) 区切りの CSV ファイルの場合の利用が紹介されています。 CSV ファイルの区切り文字は、 gnuplot では set datafile で指定できるのですが、 それはコマンドレベルでの実行なので、 一つの plot で同時にグラフを描画させるときに set datafile を割り込ませる仕組みがなく、 今までは事前にデータファイルの形式を変更するしかありませんでした。 それを関数ブロックで解決する例として、
function $set_csv(char) << EOF
set datafile separator char
EOF
plot tmp=$set_csv(",") FILE1,
tmp=$set_csv(";") FILE2
plot tmp=$set_csv(","), FILE1,
tmp=$set_csv(";"), FILE2
(cf. 「情報やメモ (08/29 2023)」)
05/21 頃に gnuplot-5.4.7 が公開されました。 5.4.7 での新規機能、変更、修正は以下のようです。
- 修正: 疑似ファイル '+', '++' では "set datafile columnheader" を無視 (#2585)
- 修正: 配列からのデータでは "set datafile columnheader" を無視 (#2585)
- 修正: 境界のない繰り返し (iteration) の plot での様々な問題 (#2589)
- 修正: plot ... smooth acsplines with filledcurves を許可 (#2592)
- 修正: "plot title at {end|beginning}" を KEYSAMPLE のレイヤーに
- 修正: csv ファイルの最後のフィールドの空文字列の処理
- 修正: 等高線生成時の非線形軸の処理 (#2593)
- 修正: yerrorbars の凡例サンプルがグラフのバーと一致するように (#2598)
- 修正: "plot with table" では平滑化操作をすべてスキップするように (#2610)
- 修正: cairolatex/epslatex: 不透明 textbox 内の文字列の重なりを防ぐ
- 修正: wxt: 3.0 より前のバージョンで XDG をサポートしていない (#2587)
- 修正: wxt: fontscale と fontsize の処理が矛盾していた (#2373)
- 修正: tikz epslatex cairolatex: TeXLive2023 での作業に更新 (#2613)
- 修正: 空配列の要素数を正しく 0 と返すように (#2616)
- 修正: 配列からの plot では datafile separator を無視
- 修正: pm3d のオプションの "at b" や "at t" と "depthorder" の組み合わせ
- 修正: 'autotitle columnhead' と 'using col("key")' の組み合わせ (#2620)
- 修正: $HOME がないために XDG ファイルが見つからない場合の警告の抑制 (#2623)
- 修正: windows terminal: アスペクト比に関して arrow の長さを補正 (#2565)
今回は細かい修正のみです。 なお、これが 5.X 系列としては最後のリリース版で、 次期リリース版のバージョンは 6.0 になる予定です (今度こそ)。
5.4.7 の all.dem の出力も置いておきます。
- all.dem の PDF 出力 (5.4.7)
all-547-20230524.pdf (780 ページ、19,577,185 Byte) - その画像を小さくした一覧 (5.4.7)
all-20230524-list.pdf (13 ページ、38,851,857 Byte)
前回の 5.4.6 用のもの (「情報やメモ (02/13 2023)」) と比較すると、419 ページ目のもの (pm3d.dem) が、 419 ページ目と 420 ページ目の 2 つに変更されているようです。 5.4.6 では「set pm3d at bstbst」のサンプルだったものを、 「set pm3d at bst border lt -1 lw .3」で境界をつけて、さらに 「set pm3d depthorder」としたものと「set pm3d interp 2,2」としたものの 2 つのサンプルに変更した、といった感じです。
今回は、昔書いた、横向きの帯グラフ (ヒストグラム) (「情報やメモ (02/07 2015)」) に関する別解を考えてみたいと思います。 実は、以下のようなものをたまたまネット上で見つけたのがきっかけです。
- gnuplotでHorizontal histogramを描く (@Torricelli_1107 さん)
https://qiita.com/Torricelli_1107/items/2b5a1ce8870e734cf378 (2022-03-09) - Horizontal histogram in gnuplot (stack overflow の質問)
https://stackoverflow.com/questions/11266452/horizontal-histogram-in-gnuplot (2012-06-29)
これは、私が以前 「情報やメモ (02/07 2015)」 に書いた、「文字を回転することで擬似的にグラフは縦に描いて できた画像を回転する」という方法ではなく、 「with boxxyerrorbars を利用して自前で横向きのグラフを描く」 という方法を用いています。 なるほどと思いましたので、過去に描いたものをそれでやるとどうなるか とやってみました。
まず、gnuplot 5.0 以前の「boxxyerrorbars」という名前は、 gnuplot 5.2 以降では「boxxyerror」に変更されていることに注意が必要です。
boxxyerror は、4 列、または 6 列のデータを必要としますが、4 列ならば、 「x, y, xdelta, ydelta」で、(x,y) を中心とする、 それぞれの辺の長さが 2*xdelta, 2*ydelta の長方形を描きます。 よって、長方形の中心と幅を計算する関数を使えば、 横向き棒グラフを描くことができます。データは、前と同じ、
年号 第一次産業 第二次産業 第三次産業
1920 54.9 20.9 24.2
1940 44.6 26.2 29.2
1960 32.7 29.1 38.2
1980 10.9 33.6 55.4
2000 5.1 29.8 65.1
を利用します。
例えば 1920 年のところの最初の棒グラフ (第一次産業) は、
x = 54.9/2, y = 1920, xdelta = 54.9/2, ydelta = 5に描き、2 つ目の棒グラフ (第二次産業) は、
x = 54.9 + 20.9/2, y = 1920, xdelta = 20.9/2, ydelta = 5として描くことになります。よって、各 j = 2,3,4 列のデータに対して、
csum(n) = sum [i=2:n] column(i)
pcj(j) = csum(j-1) + column(j)*0.5
xdel(j) = column(j)*0.5
svalue(j) = sprintf("%.1f%%", column(j))
- csum(n) は 2 列目から n 列目までの値の和を求めるもの
- pcj(j) は j 列目のデータの boxxyerror の x の位置
- xdel(j) は xdelta の値
- svalue(j) は pcj(j) の場所に書く j 列目の数字
なお、 「情報やメモ (02/07 2015)」 では、この csum(j) は再帰を利用して作っていました (colsum(n)) が、 ここでは gnuplot 4.6 以降に実装されている sum を利用しています。 これで、以下のようにすれば、ヒストグラムの部分は完成します。
set term wxt
set title "産業別就業者数(15歳以上)の構成率の変化"
font ",16"
ydel = 5 # ydelta
set ytics 1920, 20, 2000
set yrange [2020:1880] # 逆向きにして上を少し空ける
csum(n) = sum [i=2:n] column(i)
pcj(j) = csum(j-1) + column(j)*0.5
xdel(j) = column(j)*0.5
svalue(j) = sprintf("%.1f%%", column(j))
set style fill solid 0.5 border -1
set xrange [0:100]
set noxtics
set x2tics 20 # 軸の刻みを上に書く
set grid noxtics noytics x2tics lt -1 # grid は縦のみ
set x2label "(%)"
set ylabel "(年)" rotate by 0
# rotate by 0 がないと wxt では横になるし、かっこも全角でないと化ける
plot for [j=2:4] "fille"
using (pcj(j)):(column(1)):(xdel(j)):(ydel) \
with boxxyerror title columnheader(j),\
for [j=2:4] ""
using (pcj(j)):(column(1)):(svalue(j)) with labels
font ",8" notitle
- 上の実行結果 (wxt terminal のスナップショット)
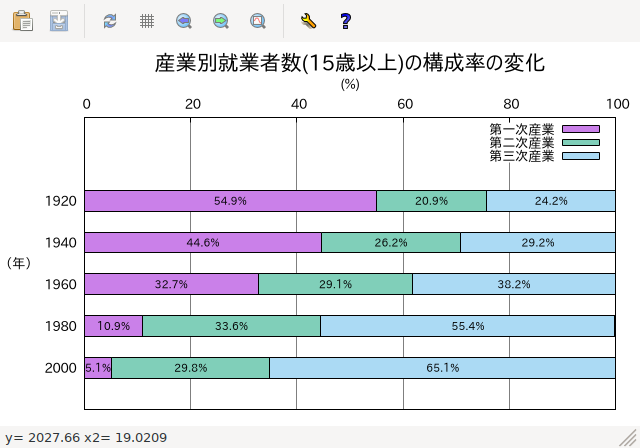
案外簡単に棒グラフ部分が再現されていることがわかります。 後は接続線です。概念としては、with vectors (x,y,xdelta,ydelta) を使って、
for [j=2:4] "" using (前の行の csum(j)):
(前の行の column(1) + ydel):\
(csum(j) - 前の行の csum(j)):
(column(1) - ydel - 前の行の column(1) - ydel) with vectors \
nohead lt -1 dt 2 not
(j, 行) = (2,2), (2,3), (2,4), (2,5), (2, 6),つまり、j=2 に対する plot を実行し、 次に j=3 に対する plot を実行し、 最後に j=4 に対する plot を実行する、 という順で行っているようです。 ということは、カンマ演算子で、現在の値を別な変数に残す、 ということをやっていけばなんとかなりそうですが、 最初の行に対する描画が行われないようにする必要がありますので、 そこだけ NaN で初期化するようにします。
(3, 2), (3,3), (3,4), (3,5), (3, 6),
(4, 2), (4,3), (4,4), (4,5), (4, 6)
ylast = 0
plot ... ,
for [j=2:4] "" using
(xlast=(column(0)==0)?NaN:xlast, xlast):\
(ylast + ydel):\
(xl=xlast, xlast=csum(j), csum(j) - xl):\
(yl=ylast, ylast=column(1), column(1) - yl - 2*ydel)\
with vectors ...
- 1 行目: (x, y, xdelta, ydelta) = (NaN, 0+5, 54.9-NaN, 1920-0-10), (xlast, ylast) = (54.9, 1920)
- 2 行目: (x, y, xdelta, ydelta) = (54.9, 1920+5, 44.6-54.9, 1940-1920-10), (xlast, ylast) = (44.6, 1940)
- 5 行目: (x, y, xdelta, ydelta) = (10.9, 1980+5, 5.1-10.9, 2000-1980-10), (xlast, ylast) = (5.1, 2000)
これで適切な接続線が描かれることがわかると思います。 そして次に j=3 では以下のようになります。
- 1 行目: (x, y, xdelta, ydelta) = (NaN, 2000+5, 54.9+20.9-NaN, 1920-2000-10) (xlast, ylast) = (54.9+20.9, 1920)
- 2 行目: (x, y, xdelta, ydelta) = (54.9+20.9, 1920+5, 44.6+26.2-(54.9+20.9), 1940-1920-10), (xlast, ylast) = (44.6+26.2, 1940)
1 行目の y や ydelta は不正な値になりますが NaN があるので描画されず、 2 行目から正しい値になるのでこれで適切な接続線が描かれます。 結局以下のようにして接続線付きの帯グラフが完成します。
set term wxt
set title "産業別就業者数(15歳以上)の構成率の変化"
font ",16"
ydel = 5 # ydelta
set ytics 1920, 20, 2000
set yrange [2020:1880] # 逆向きにして上を少し空ける
csum(n) = sum [i=2:n] column(i)
pcj(j) = csum(j-1) + column(j)*0.5
xdel(j) = column(j)*0.5
svalue(j) = sprintf("%.1f%%", column(j))
set style fill solid 0.5 border -1
set xrange [0:100]
set noxtics
set x2tics 20 # 軸の刻みを上に書く
set grid noxtics noytics x2tics lt -1 # grid は縦のみ
set x2label "(%)"
set ylabel "(年)" rotate by 0
# rotate by 0 がないと wxt では横になるし、かっこも全角でないと化ける
ylast = 0
plot for [j=2:4] "fille"
using (pcj(j)):(column(1)):(xdel(j)):(ydel) \
with boxxyerror title columnheader(j),\
for [j=2:4] ""
using (pcj(j)):(column(1)):(svalue(j)) with labels
font ",8" notitle,\
for [j=2:4] ""
using (xlast=(column(0)==0)?NaN:xlast,xlast):(ylast+ydel):\
(xl=xlast,xlast=csum(j),csum(j)-xl):\
(yl=ylast,ylast=column(1),column(1)-yl-2*ydel) \
with vectors nohead lt -1 dt 2 not
- 上の実行結果 (wxt terminal のスナップショット)
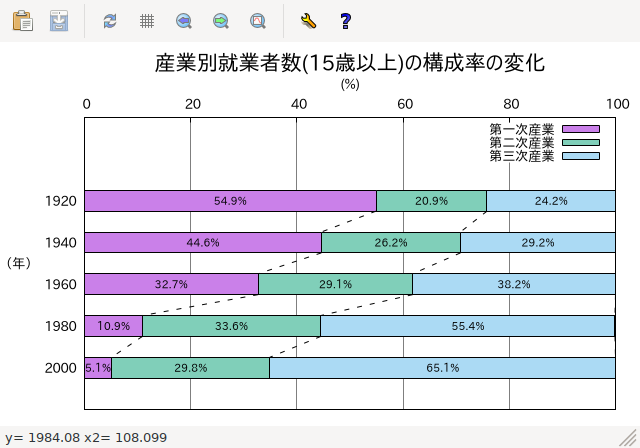
以前の回転による方法よりも見通しはいいですし、 wxt terminal でも容易に確認ができるのがいいです。 key の自作も必要ありません。 この方法であれば、色々な横向き棒グラフ、 ヒストグラムが実現できそうです。
(cf. 「情報やメモ (09/29 2023)」)
最新の開発版 (git) の all.dem の出力を置いておきます。
- all.dem の PDF 出力 (2023-04-05 の GIT 版)
all-current-20230407.pdf (771 ページ、26,162,106 Byte) - その画像を小さくした一覧 (2023-04-05 の GIT 版)
all-20230407-list.pdf (13 ページ、36,519,455 Byte)
「情報やメモ (01/25 2023)」 の時点でのデモ (755 ページ) に比べると、かなり変更があります。
- 新規の concave_hull.dem の分 (58-62 ページ)
- 新規の sectors.dem の分 (134-147 ページ)
- pm3d_clip.dem に追加された分 (498 ページ)
- rgbalpha.dem が削除された分の削除 (旧ファイルの 634-635 ページ)
- circles.dem のデモが 2 つ削除 (旧ファイルの 659-660 ページ)
concave_hull.dem, sectors.dem は今回新規に導入された機能で、 そのための多くのデモが追加されています。 498 ページに追加されているのは、2 つの曲面の滑らかな交差のデモで、 2 曲面のグラフや、自分自身と交差する曲面、 平面と交差する曲面のグラフデモなどは従来もありましたが、 この形のものは今まではなかったようです。 また、他にも入れ替わってはいなくても、 表示が少し変更されているものもあります (例えば 756-759 ページ等)。
この間 (2023-01-25 以降) の git 版の改変としては、 以下のようなものがあるようです。 なお、ドキュメントの差分で見ているので、 変更はほかにもあると思います。
- with sectors の新設
- with pm3d のオプション zclip の新設
- フィルタ concavehull (chi-shape) の新設
- arrowstyle valiable の新設
- splot with boxes による 3 次元 box の境界色を set pm3d border から fill style の border に変更
1. は新しい描画スタイルで、データの各点に対し、 バームクーヘンのかけらのような扇片を描きます。 線ではなく図形を描く、という点では with circles や with ellipses に近いものと言えますが、 この with sectors は扇型を方向θと半径 r、 方向の変位Δθと半径の変位Δr、 そして必要ならば中心座標 cx,cy を指定して描画できるものです。 座標系は、直交座標上でも極座標上でも描けます。
これにより、円グラフ/円環グラフも描けますし、鶏頭グラフや色見本、 ダイヤルチャートなども簡単にかけます。 しかも、直交座標上で複数の円グラフが簡単に描けるので、 表現できることがだいぶ増えます。 デモの 134-147 ページをご覧ください。 なお、開発したのは日本の方 (Hiroki Motoyoshi さん) のようで、 開発版のマニュアルでは、開発者リストに新規に名前が加えられています。
2. は 3 次元グラフの z 方向のクリッピングで、 その境界が滑らかになるように切ります。 ドキュメントには、これと do for を組み合わせたアニメーションの例が載っています。 3 次元グラフを上から順番に水平に切り落としていくようなものです。
3. は、「convex hull」(凸包) なら知っていますが、 「concave hull」(凹包) は私は初耳です。 既に実装されている convexhull フィルタに対応して新設されたフィルタです。 chi_length というパラメータがあり、 それに応じて形も変化するもののようで、 一般には凸とは限らない図形になります。 指定したデータを全部中に含むような閉曲線であることは凸包と同じですが、 そこから作られるドロネー三角形分割から、 パラメータに応じて三角形をいくつか削除して作られるχ-形状 (chi-shape) と呼ばれる閉曲線を作成するようです。 点集合全体のおおまかな形を知るためには、 凸包よりもいいのかもしれません。
4. は、追加列で arrowstyle の index 番号を 指定できるようになったものです。 これで with vectors や with arrows による 1 回の plot で、 多くの種類のベクトルや矢を表示できるようになります。
(cf. 「情報やメモ (05/30 2023)」)
gnuplot による単振り子のシミュレーションの例を紹介します。 これは import を使用するので、そのサンプルにもなると思います。 なお、import のサンプルは、以下の、例えば松田さんのサイト、 米澤さんのサイトでも紹介されています。
- import:外部ライブラリ内の関数呼び出し (松田七美男さん)
- C 言語の関数を取り込む (import) (米澤進吾さん)
単振り子は、長さ l の軽いひもに質量 m のおもりをつけて原点に結んで 揺らした振り子の運動です。\(u\) を鉛直方向に対する振れ角とすると、 おもりの位置は \((x,y) = l(\sin u,\cos u)\) となり、 重力加速度を g とすると、まさつや空気抵抗を無視すれば、 \(u=u(t)\) (t: 時刻) に対する運動方程式は \[ mlu'' = -g\sin u \] となります。 初期値を \(u(0)=u_0\in(0,\pi), u'(0)=0\) とすると、 この方程式の解は楕円関数で表現できることが知られています。 \(k=\sin(u_0/2)\) とすると、振り子の周期は \(T=4K(k)\sqrt{l/g}\) で、 \(K(k) = F(\pi/2,k)\) は第一種完全楕円積分、 \(F(\phi,k)\) は第一種不完全楕円積分 \[ F(\phi,k) = \int_0^{\phi}\frac{d\phi}{\sqrt{1-k^2\sin^2\phi}} \] であり、解は、 \[ u=2\sin^{-1}(k\times \mathrm{sn}(K(k)(1-4t/T)),k)) \] となります。ここで、\(\mathrm{sn}(u,k)\) はヤコビの楕円関数で、 \(u=F(\phi,k)\) の \(\phi\) に関する逆関数 \(\phi=F^{-1}(u;k)\) を用いて \[ \mathrm{sn}(u,k) = \sin(F^{-1}(u;k)) \] と表すこともできます。 なお、\(\mathrm{sn}(u,k)\) は、 複素変数の関数と考えれば二重周期関数ですが、 実変数の関数としては、周期は 4K(k) です。
gnuplot には完全楕円積分 \(K(k)\) は用意されていますが、 \(F(\phi,k)\) や \(\mathrm{sn}(u,k)\) は用意されていません。 それを、数値ライブラリの GNU gsl を利用し import して用いることにします。
なお、高校の物理等では、この単振り子の方程式は、 振れ角 \(\theta\) が小さい場合を考え \(\sin\theta\) を \(\theta\) で近似し 単振動として考えて等時性などを示したりします。 その場合、周期は \(T=2\pi\sqrt{l/g}\)、解は \[ u=u_0\cos(2\pi t/T) \] です。比較のためにこれも合わせてシミュレートしてみます。
gnuplot で import するためには、 gnuplot と gsl とのなかだちをする共有ライブラリが必要で、 C 言語で gnuplot 用のインターフェースを備えた関数を作る必要があり、 その書き方はサンプルが demo/plugin 内に demo_plugin.c として含まれているので、それを参考にすればいいでしょう。 なお、そこには Makefile.am もありますが、 これは autoconf 用のファイルで、 同様のものを書いて Makefile を生成させることも可能ですが、 直接 Makefile を書くことも難しくはないので、 ここでは Makefile のサンプルも紹介します (FreeBSD 用)。 また、demo/plugin に含まれる gnuplot_plugin.h も必要です。
gsl ライブラリは /usr/local/ にインストールされているとしていて、 FreeBSD の場合は -lgsl の後ろに -lgslcblas も必要です。 gmake clean として gmake とすると gsl1.so ができます。 使用している gsl の関数等については、 gsl1.c のコメントを参照してください。 そして、これを import すれば、 gnuplot 内で第 1 種不完全楕円積分を myincF(t,k)、 ヤコビの楕円関数は mysn(u,k) として利用できます。
単振り子の周期を T1, 線形近似の周期を T2 として、 以下のようにして両者の振れ角を表示できます。
import myincF(t, k) from "gsl1"
import mysn(t, k) from "gsl1"
myK(k) = EllipticK(k) # gnuplot の第一種完全楕円積分
g = 9.8
l = 1.0
u0 = 0.25*pi
k0 = sin(0.5*u0)
T1 = 4.0*myK(k0)*sqrt(l/g)
T2 = 2.0*pi*sqrt(l/g)
u1(t, k) = 2*asin(k*mysn(myK(k)*(1.0-4.0*t/T1), k))
u2(t) = u0*cos(2.0*pi*t/T2)
set grid
set samples 500
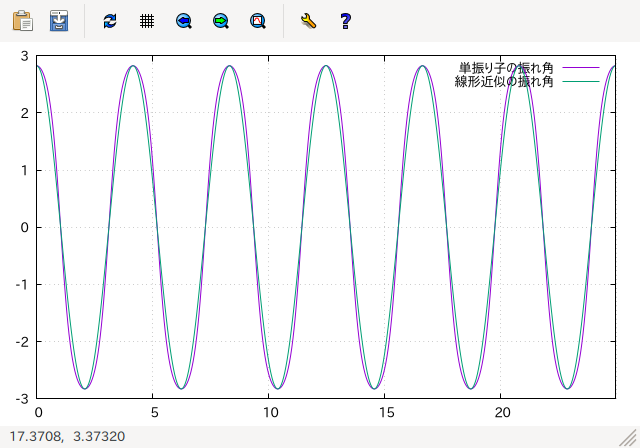
plot [0:6*T1] u1(x, k0) t "単振り子の振れ角",\
u2(x) t "線形近似の振れ角"
- 単振り子と線形近似の振れ角のグラフ
(wxt terminal のスクリーンショット)
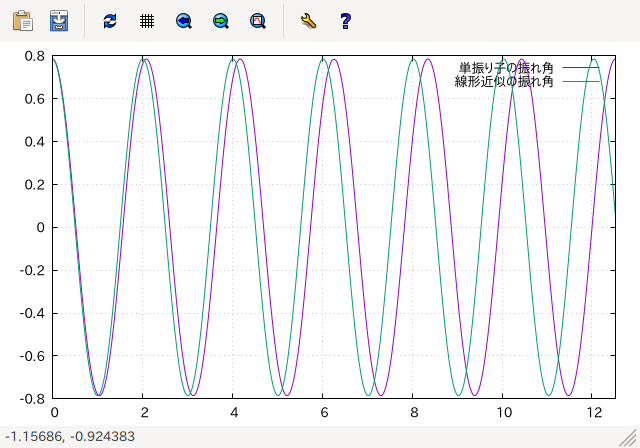
グラフを見ると、初期角 u0 が 0 には近くないため、 線形近似とはずれがあり、 単振り子の周期の方が線形近似の周期よりも少し長いことがわかります。 u0 をさらに大きくすれば、線形近似とのずれはより大きくなります。
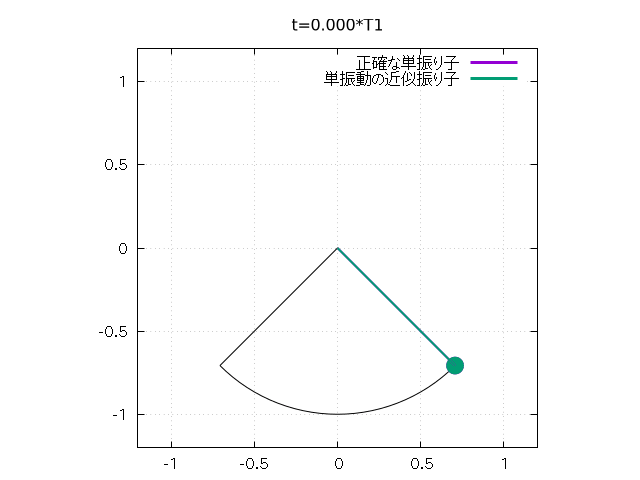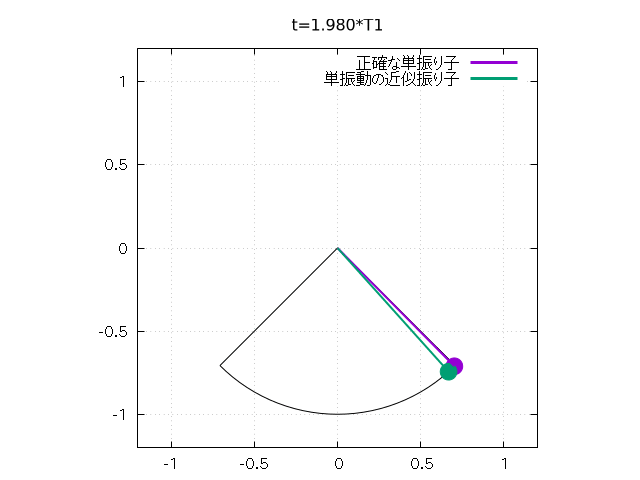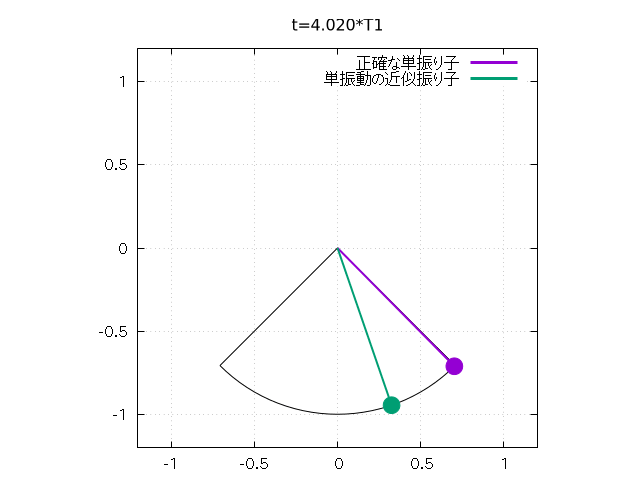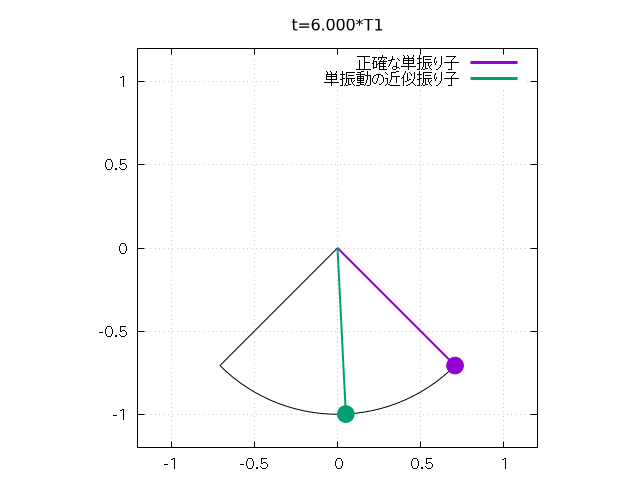
さらに以下のようにして、 振り子の振れをアニメーションで再現することもできます。
set size square
set xrange [-l*1.2:l*1.2]
set yrange [-l*1.2:l*1.2]
Tlast = 6.0*T1 # 出力最終時刻
N = 100 # 時間分割数
set object 1 circle at 0,0 size l \
arc [(-u0-pi/2)*180/pi:(u0-pi/2)*180/pi] \
fs empty border lt -1
# 振り子の軌道
dt = Tlast/N
csz = 0.05 # おもりのサイズ
do for [j=0:N] {
unset arrow 2; unset object 3; unset arrow 4;
unset object 5
t = j*dt
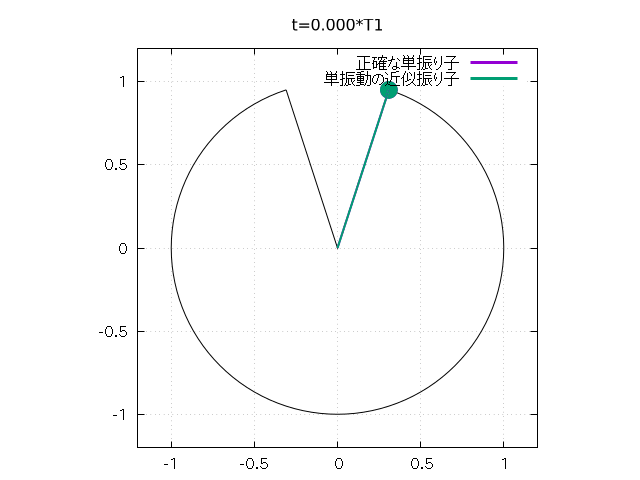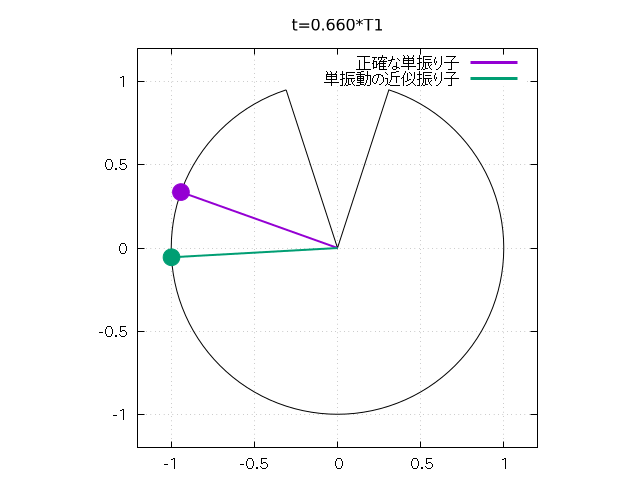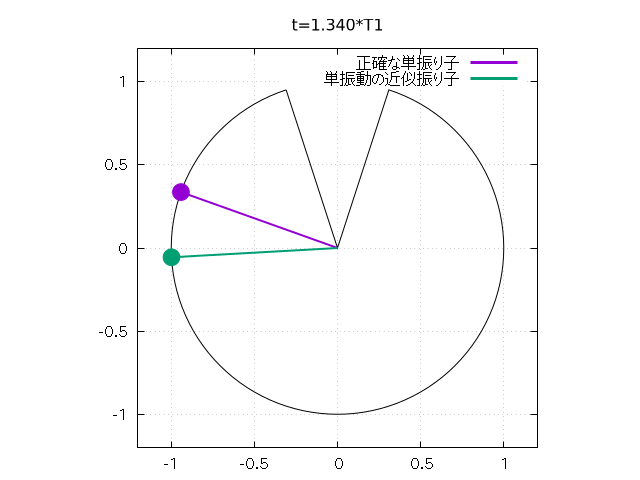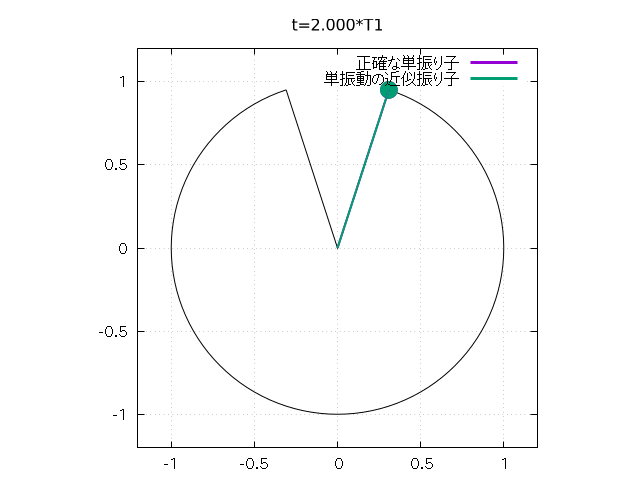
set title sprintf("t=%.3f*T1", t/T1)
u = u1(t, k0)
a = l*cos(u - pi/2.0); b = l*sin(u - pi/2.0)
set arrow 2 from 0,0 to a,b nohead lt 1 lw 2
set object 3 circle at a,b size csz fs solid fc lt 1
# arrow と circle で単振り子を表現
u = u2(t)
a = l*cos(u - pi/2.0); b = l*sin(u - pi/2.0)
set arrow 4 from 0,0 to a,b nohead lt 2 lw 2
set object 5 circle at a,b size csz fs solid fc lt 2
# こちらは線形近似
plot 1/0 w l lt 1 lw 3 t "正確な単振り子", \
1/0 w l lt 2 lw 3 t "単振動の近似振り子"
# 1/0 の空打ちで arrow, object の描画と key の描画
}