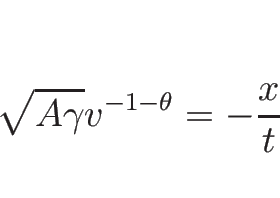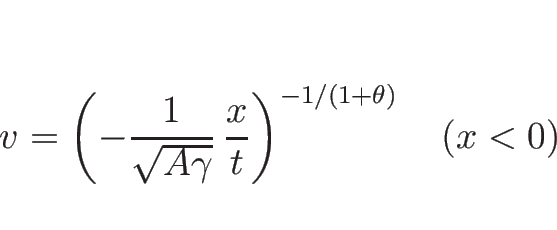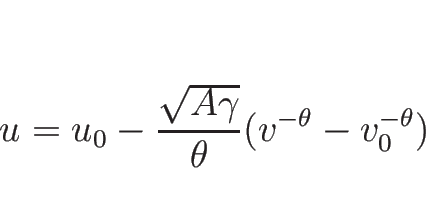3.8 バロトロピックのラグランジュ座標系の場合の例
3.7 節と同様に、
ラグランジュ座標系の方程式系 (2.19) の圧力を
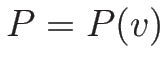 と見て、最初の 2 本のみ (いわゆる
と見て、最初の 2 本のみ (いわゆる 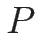 -system) を同様に考察する。
この場合も通常は
-system) を同様に考察する。
この場合も通常は
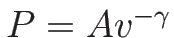 (
(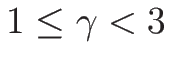 ) を想定していて、
) を想定していて、
を仮定することが多い。
方程式を
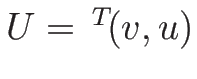 で書けば
で書けば
で、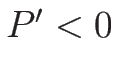 であれば固有値は
であれば固有値は
であり、固有ベクトルは
で、
より、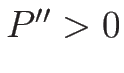 であれば 1-特性方向、2-特性方向は真性非線形となる。
であれば 1-特性方向、2-特性方向は真性非線形となる。
リーマン不変量は、
より、
から、
となるので、
が 1-リーマン不変量となる。
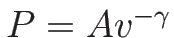 (
(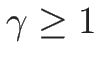 ) の場合は、
) の場合は、
となる。
ここから、3 本の連立方程式の場合と同様、
オイラー座標系の場合のリーマン不変量に対応していることがわかる。
2-リーマン不変量も同様に
と得られる。
1-膨張波曲線 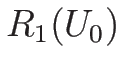 は、
は、
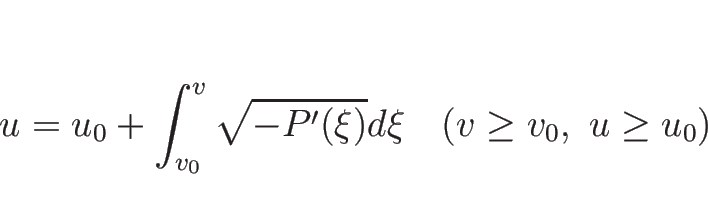 |
(3.48) |
2-膨張波曲線 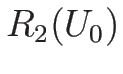 は、
は、
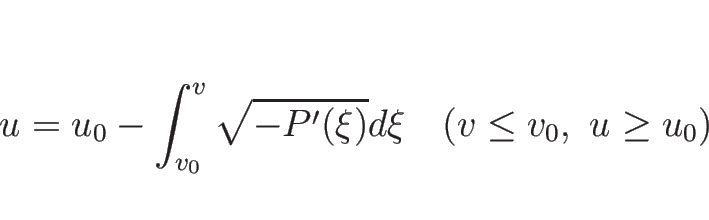 |
(3.49) |
となる。
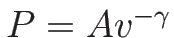 (
(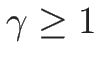 ) の場合、
) の場合、
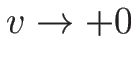 のときは
のときは 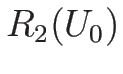 は
は 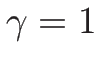 でも
でも 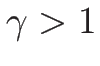 でも
でも
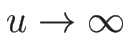 となるが、
となるが、
 のときの
のときの 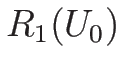 は、
は、
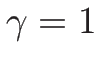 と
と 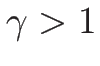 では様子が異なり、
では様子が異なり、
となる。
また、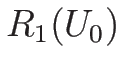 の場合は (3.29) より、
の場合は (3.29) より、
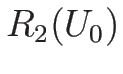 の場合は (3.30) より、
の場合は (3.30) より、
なので、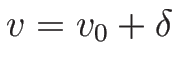 ,
, 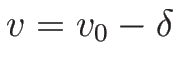 とすれば
とすれば 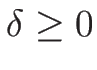 で、
で、
が成り立つ。
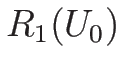 を
を 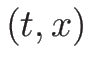 で表わすには、
で表わすには、
を 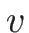 で解けば
で解けば 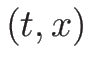 で表わされ、
それを (3.29) に代入すれば
で表わされ、
それを (3.29) に代入すれば 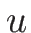 も
も 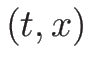 で
表される。
同様に
で
表される。
同様に 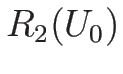 も、
も、
を 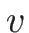 で解いて、それを (3.30) に
代入すれば
で解いて、それを (3.30) に
代入すれば 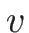 ,
, 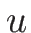 が
が 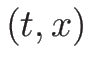 で表される。
で表される。
例えば、
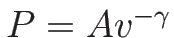 (
(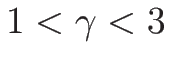 ) の場合、
) の場合、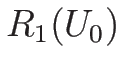 は
は
より
であり、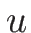 は
は
にそれを代入して得られる。
竹野茂治@新潟工科大学
2018-08-01
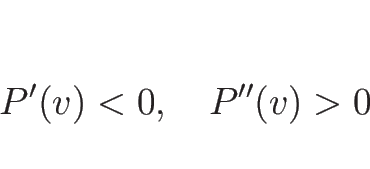
![]() で書けば
で書けば
![\begin{displaymath}
\left[\begin{array}{c}v\\ u\end{array}\right]_t
+\left[\begi...
...ray}\right]
\left[\begin{array}{c}v\\ u\end{array}\right]_x
=0
\end{displaymath}](img485.png)
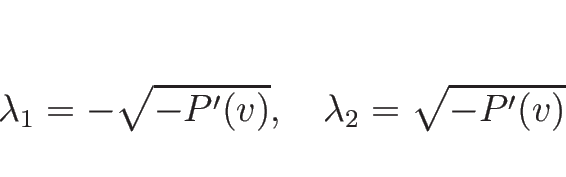
![\begin{displaymath}
r_1=\left[\begin{array}{c}1\\ \sqrt{-P'(v)}\end{array}\right...
...r_2=\left[\begin{array}{c}-1\\ \sqrt{-P'(v)}\end{array}\right]
\end{displaymath}](img488.png)
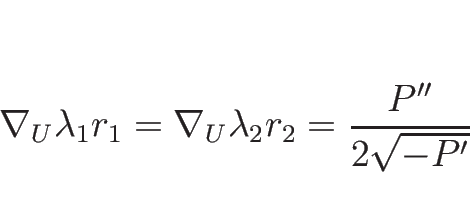
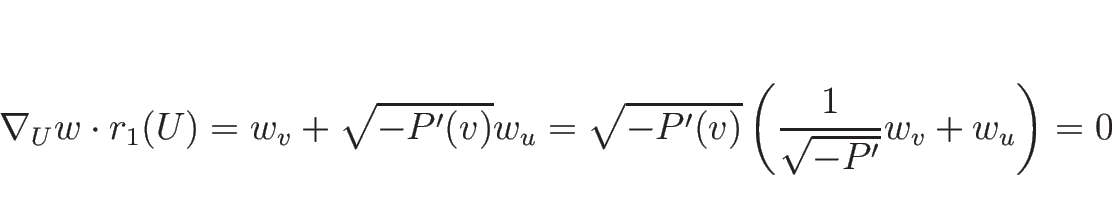
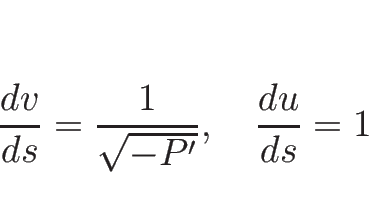
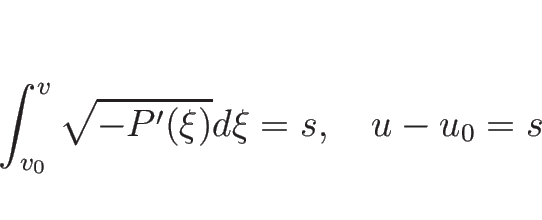
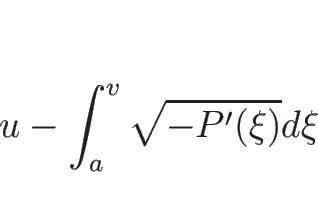
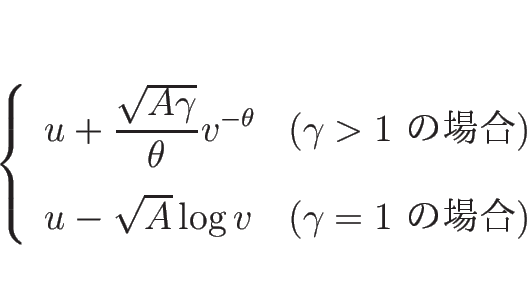
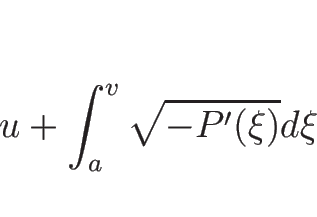
![]() は、
は、
![\begin{displaymath}
u\rightarrow
\left\{\begin{array}{ll}
\displaystyle u_0+\fr...
...[.5zh]
+\infty & (\mbox{$\gamma=1$\ のとき})\end{array}\right.\end{displaymath}](img464.png)
![]() の場合は (3.29) より、
の場合は (3.29) より、
![\begin{displaymath}
\frac{d U}{d v}=\frac{d}{d v}\left[\begin{array}{c}v\\ u\end...
...=\left[\begin{array}{c}1\\ \sqrt{-P'}\end{array}\right]=r_1(U)
\end{displaymath}](img503.png)
![\begin{displaymath}
\frac{d U}{d v}=\frac{d}{d v}\left[\begin{array}{c}v\\ u\end...
...left[\begin{array}{c}1\\ -\sqrt{-P'}\end{array}\right]=-r_2(U)
\end{displaymath}](img504.png)
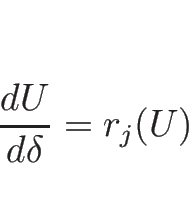
![]() を
を ![]() で表わすには、
で表わすには、
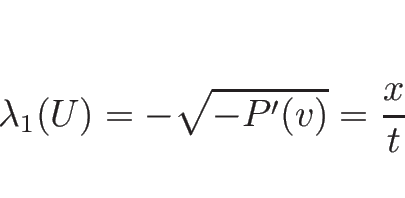
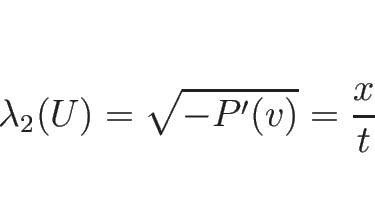
![]() (
(![]() ) の場合、
) の場合、![]() は
は