4 一般の錐体の場合の極座標公式
3 節の錐体は、円錐を斜めに切ったものであり、
この場合は展開図は簡単に極座標表示できたが、
斜円錐、すなわち底面が円で、
頂点がその中心の真上にない点である錐体の場合は、
展開図を与える式はそのように簡単にはならない。
それは、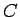 のパラメータ
のパラメータ 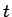 と
展開図の極座標の中心角
と
展開図の極座標の中心角 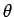 との間に (3) のような簡単な関係式が成り立たないからである。
との間に (3) のような簡単な関係式が成り立たないからである。
本節では、まず一般的な錐体に対してその 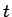 と
と 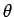 の関係式を求め、
展開図の極座標による表現式を与えることを考える。
の関係式を求め、
展開図の極座標による表現式を与えることを考える。
まず、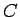 上の点をパラメータ
上の点をパラメータ 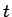 を用いて
を用いて
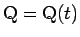 (
(
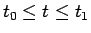 ) で表し (
) で表し (
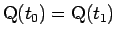 )、
)、
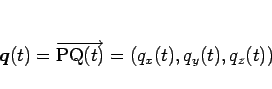
とし、その母線の長さを
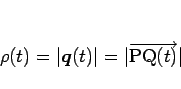
とする (図 6)。
そして、側面を母線
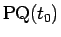 で切り開いた展開図は、
頂点
で切り開いた展開図は、
頂点 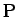 を原点に合わせ、
を原点に合わせ、
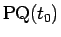 を
を 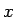 軸に合わせ、
曲線
軸に合わせ、
曲線 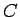 に対応する展開図の曲線を
に対応する展開図の曲線を 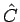 とし、
とし、
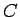 上の点
上の点 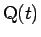 に対応する展開図上の点を
に対応する展開図上の点を
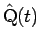 とする (図 7)。
この
とする (図 7)。
この 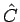 を極座標表示することを考える。
を極座標表示することを考える。
今、
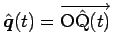 とすると、まず
とすると、まず
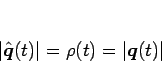 |
(7) |
であり、そして
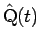 を決めるもう一つの条件は、
を決めるもう一つの条件は、
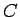 上の弧
上の弧
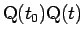 の長さが、
の長さが、
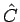 上の弧
上の弧
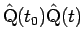 の
長さに等しいことであり、それは、
の
長さに等しいことであり、それは、
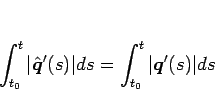
と書けるので、この両辺を 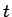 で微分すれば、
で微分すれば、
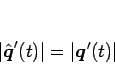 |
(8) |
となる。この (7), (8) と、
初期条件
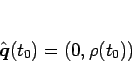 |
(9) |
によって
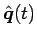 、すなわち
、すなわち
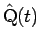 が決まることになる。
が決まることになる。
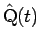 を極座標
を極座標 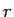 ,
, 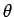 で表すことを考え、
で表すことを考え、
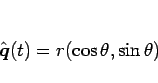 |
(10) |
とすると、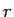 と
と 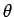 を
を 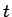 で表すことができる。
その
で表すことができる。
その 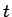 を消去すれば、展開図
を消去すれば、展開図 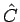 を
を 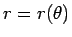 の形の
極座標で表すことができることになる。
の形の
極座標で表すことができることになる。
まず、(7) より
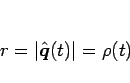 |
(11) |
であり、
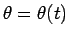 とすると、(10) より、
とすると、(10) より、
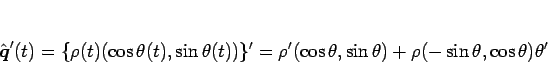
となるので、
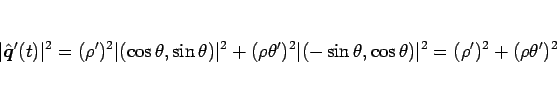
より、(8) から
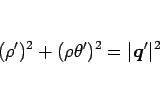 |
(12) |
となる。
ここで、(7) より、
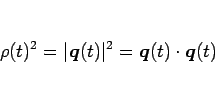
であるから、これを微分すれば
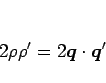
となるので、
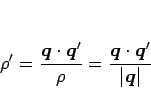
と書ける。よって (12) より

となるから、題意より 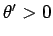 なので、
なので、
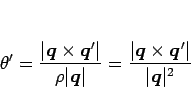
となり、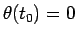 より結局
より結局 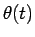 は
は
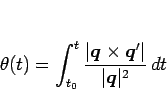 |
(13) |
と表されることになる。
この (11), (13) から 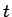 を消去する、
あるいは
を消去する、
あるいは 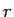 ,
, 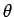 のパラメータ
のパラメータ 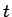 による表現により
による表現により
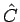 が得られるわけであるが、
この積分 (13) の計算は必ずしも易しくはないことに注意する。
が得られるわけであるが、
この積分 (13) の計算は必ずしも易しくはないことに注意する。
今、3 節の例にこれを適用してみよう。
この場合は、(6) の右辺が
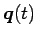 なので、
簡単のため、
なので、
簡単のため、
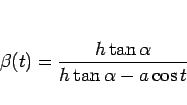
とすると
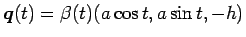 であるから、
であるから、
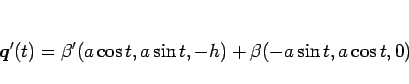
であるから、
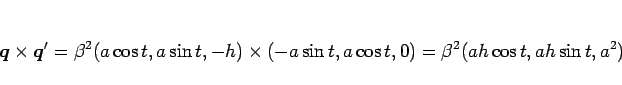
となる。よって、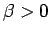 より
より
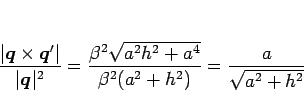
となるので、(13) より
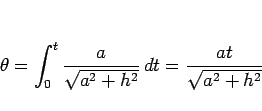
となり、
確かに 3 節の (3) が得られることになる。
竹野茂治@新潟工科大学
2009年9月18日
![]() と
と ![]() の関係式を求め、
展開図の極座標による表現式を与えることを考える。
の関係式を求め、
展開図の極座標による表現式を与えることを考える。
![]() 上の点をパラメータ
上の点をパラメータ ![]() を用いて
を用いて
![]() (
(
![]() ) で表し (
) で表し (
![]() )、
)、
![]() で切り開いた展開図は、
頂点
で切り開いた展開図は、
頂点 ![]() を原点に合わせ、
を原点に合わせ、
![]() を
を ![]() 軸に合わせ、
曲線
軸に合わせ、
曲線 ![]() に対応する展開図の曲線を
に対応する展開図の曲線を ![]() とし、
とし、
![]() 上の点
上の点 ![]() に対応する展開図上の点を
に対応する展開図上の点を
![]() とする (図 7)。
この
とする (図 7)。
この ![]() を極座標表示することを考える。
を極座標表示することを考える。
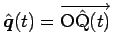 とすると、まず
とすると、まず
![]() を極座標
を極座標 ![]() ,
, ![]() で表すことを考え、
で表すことを考え、
![]() を消去する、
あるいは
を消去する、
あるいは ![]() ,
, ![]() のパラメータ
のパラメータ ![]() による表現により
による表現により
![]() が得られるわけであるが、
この積分 (13) の計算は必ずしも易しくはないことに注意する。
が得られるわけであるが、
この積分 (13) の計算は必ずしも易しくはないことに注意する。
![]() なので、
簡単のため、
なので、
簡単のため、