

Next: 8 根号内が完全平方になる場合
Up: 斜円錐の側面積について
Previous: 6 曲面積を求める公式:
(PDF ファイル: yokoyama1.pdf)
7 この積分の計算可能性
この節では、この積分 (17) の計算可能性について考察する。
ここでいう計算可能性とは、通常使われる初等的な関数等で
この積分を表すことができるか、ということを意味する。
微分とは異なり、積分はそれができないものも数多く存在する。
(17) は根号の中に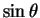 ,
, 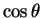 の 2 次式が
含まれているが、
例えば、より易しい積分
の 2 次式が
含まれているが、
例えば、より易しい積分
でも、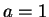 のときは半角の公式を使えば容易に積分できるが、
のときは半角の公式を使えば容易に積分できるが、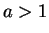 のときは
のときは
となり、この最後の式は 第 2 種楕円積分 と呼ばれる、
簡単な式では表せないことが良く知られているものになっている
(0 から 1 までの定積分なので、いわゆる 完全楕円積分 にもなっている)。
この例と同様に、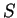 の式 (17) を
このような楕円積分の標準形に帰着させることで、
実際に簡単には計算できない式であることを示すことを目標とする。
ただし、一般の
の式 (17) を
このような楕円積分の標準形に帰着させることで、
実際に簡単には計算できない式であることを示すことを目標とする。
ただし、一般の 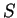 の式を考察するのはかなり大変なので、
この節では元々の問題の
の式を考察するのはかなり大変なので、
この節では元々の問題の 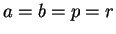 ,
, 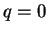 の場合のみを考えることにする。
の場合のみを考えることにする。
なお、楕円積分という名前は、元々楕円の周囲の長さを計算するときに現われる
積分を簡単な式では表すことができない、という事実に由来するが、
楕円の周の長さはまさにこの第 2 種完全楕円積分で表される。
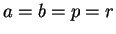 ,
, 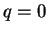 の場合、(17) は次のような式になる。
の場合、(17) は次のような式になる。
この式を
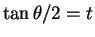 と置換することで
根号の中身を有理式に変換する。この場合、
と置換することで
根号の中身を有理式に変換する。この場合、
となるので、
となる。積分の中に
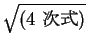 が現われるが、
一般に、多くの
が現われるが、
一般に、多くの
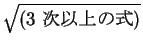 の形が含まれている積分が
楕円積分になることが知られている。
しかし、この形が現われたら常に積分できないかというとそうではない。
例えば良く知られているように
の形が含まれている積分が
楕円積分になることが知られている。
しかし、この形が現われたら常に積分できないかというとそうではない。
例えば良く知られているように
の形の積分は 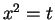 と置換することで
と置換することで
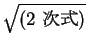 の形になり
ちゃんと簡単な式で表すことができるし、
また根号の中が完全平方式で
の形になり
ちゃんと簡単な式で表すことができるし、
また根号の中が完全平方式で
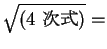 (2 次式) となる場合も
もちろん積分できる (これらの場合は 疑似楕円積分 と呼ばれる)。
よって、本当に簡単に積分できない楕円積分であることを示すには、
(2 次式) となる場合も
もちろん積分できる (これらの場合は 疑似楕円積分 と呼ばれる)。
よって、本当に簡単に積分できない楕円積分であることを示すには、
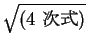 が出てくるから、というだけでは十分ではなく、
簡単な式では表すことができないことが知られている
楕円積分の標準形への変換が必要となる。
最近の書物にはあまりその変換の方法に触れたものを見かけないが、
例えば [1] 12.25「楕円積分 (I)」 にそれが書かれているので
それに従って標準形への変換を行なう。
ただし、その途中の計算を全て書きあげるとかなりの分量になるので、
適宜省略しながら計算を紹介する。
が出てくるから、というだけでは十分ではなく、
簡単な式では表すことができないことが知られている
楕円積分の標準形への変換が必要となる。
最近の書物にはあまりその変換の方法に触れたものを見かけないが、
例えば [1] 12.25「楕円積分 (I)」 にそれが書かれているので
それに従って標準形への変換を行なう。
ただし、その途中の計算を全て書きあげるとかなりの分量になるので、
適宜省略しながら計算を紹介する。
今、
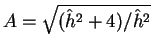 とすると,
とすると, 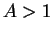 であり、
(18) の根号の部分は
であり、
(18) の根号の部分は
となる。ここでこの (18) の積分を 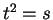 と置換すると、
と置換すると、
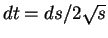 なので、
なので、
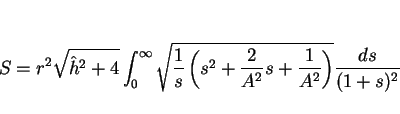 |
(19) |
となる。ここで、
に注意すると、(19) の根号部分は
と書ける。なお、
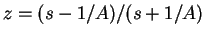 とした。
(19) の積分においてこの
とした。
(19) の積分においてこの 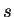 から
から 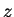 への置換を行なうと、
への置換を行なうと、
となるので、
となる。
詳しい計算は省くが、この被積分関数に対しては次のような関係式が成り立つ。
ここで、
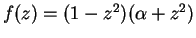 とした。もちろん、
とした。もちろん、
であり、また右辺第 2 項は、
と変形すると、最後の項は 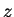 に関して奇関数なので
に関して奇関数なので 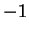 から 1 での積分の値は
0 となる。よって、結局
から 1 での積分の値は
0 となる。よって、結局 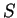 は、
は、
によって、
と表されることになる。また、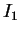 ,
, 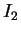 ,
, 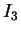 はいずれも偶関数の積分なので、0 から 1 までの積分の値を 2 倍したものに等しい。
はいずれも偶関数の積分なので、0 から 1 までの積分の値を 2 倍したものに等しい。
その 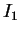 ,
, 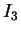 の積分で、
の積分で、
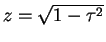 と置換する。このとき
と置換する。このとき
となるので、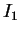 は
は
と変形でき、これは 第 1 種完全楕円積分 の形になっている。
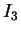 は
は
となるので、これは第 2 種完全楕円積分になる。
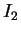 は、
は、
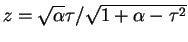 と置換する。
このとき、
と置換する。
このとき、
より、
なので、
となり、よって
となり、最後の積分は 第 3 種楕円積分 である。
なお、第 3 種楕円積分は、
を標準形とする (すなわち 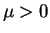 でも構わない) 流儀もあるようなので、
それにあわせるだけなら
でも構わない) 流儀もあるようなので、
それにあわせるだけなら 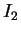 を
を 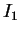 ,
, 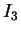 と同様に
と同様に
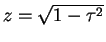 と置換して
と置換して
としてもよい。
結局、それぞれの楕円積分を
とすると、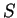 は
は
のように表されることになる。
よって、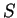 は楕円関数の標準形で書けることになり、
簡単な関数で表すことはできない、ということが言えたことになる。
は楕円関数の標準形で書けることになり、
簡単な関数で表すことはできない、ということが言えたことになる。
一般の (17) の場合も
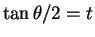 と置換すれば、
根号の中が 4 次式になるので
上の計算と同様にして標準形に変換できるかも知れないが、
その 4 次式の処理は上の場合ほど簡単にはいかずかなり難しい。
しかし、多くの場合に上の場合と同様に楕円積分になってしまうであろうことは
想像がつく。
そうはならない場合については 8 節で考察する。
と置換すれば、
根号の中が 4 次式になるので
上の計算と同様にして標準形に変換できるかも知れないが、
その 4 次式の処理は上の場合ほど簡単にはいかずかなり難しい。
しかし、多くの場合に上の場合と同様に楕円積分になってしまうであろうことは
想像がつく。
そうはならない場合については 8 節で考察する。


Next: 8 根号内が完全平方になる場合
Up: 斜円錐の側面積について
Previous: 6 曲面積を求める公式:
Shigeharu TAKENO
2005年 2月 28日
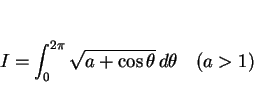
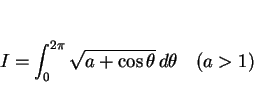
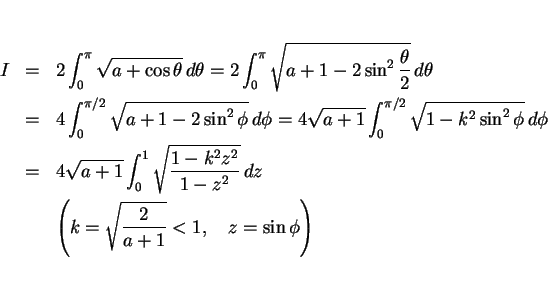
![]() ,
, ![]() の場合、(17) は次のような式になる。
の場合、(17) は次のような式になる。
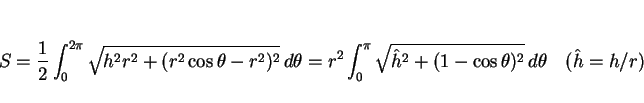
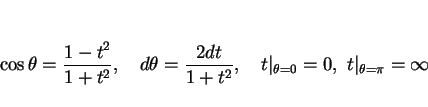
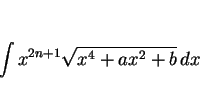
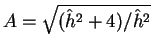 とすると,
とすると, ![]() であり、
(18) の根号の部分は
であり、
(18) の根号の部分は
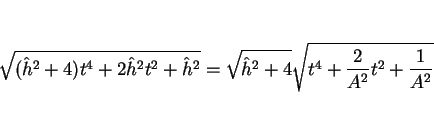

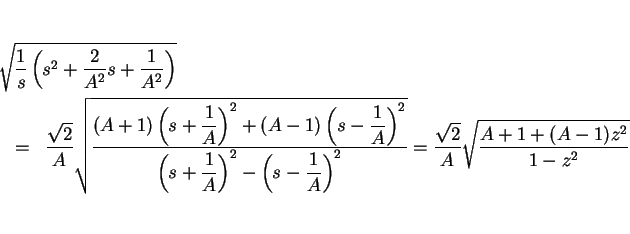
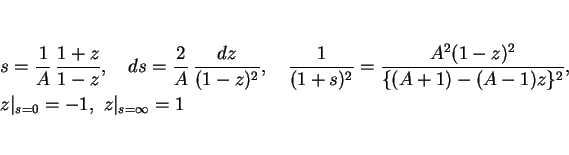
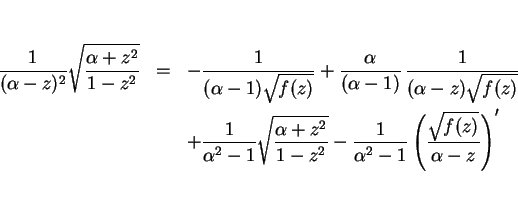
![\begin{displaymath}
\int_{-1}^1\left(\frac{\sqrt{f(z)}}{\alpha-z}\right)'\, dz
= \left[\frac{\sqrt{f(z)}}{\alpha-z}\right]_{z=-1}^{z=1}=0
\end{displaymath}](img187.gif)
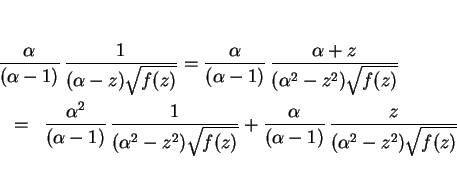
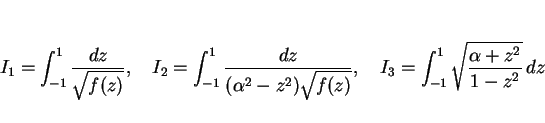
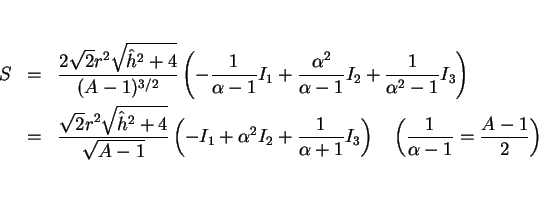
![]() ,
, ![]() の積分で、
の積分で、
![]() と置換する。このとき
と置換する。このとき
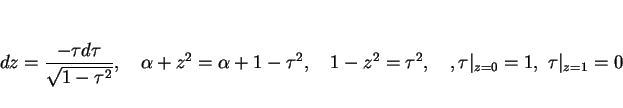
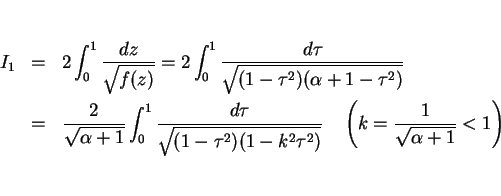
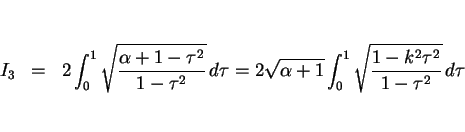
![]() は、
は、
![]() と置換する。
このとき、
と置換する。
このとき、
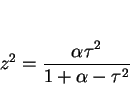
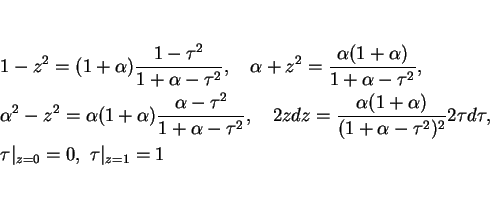
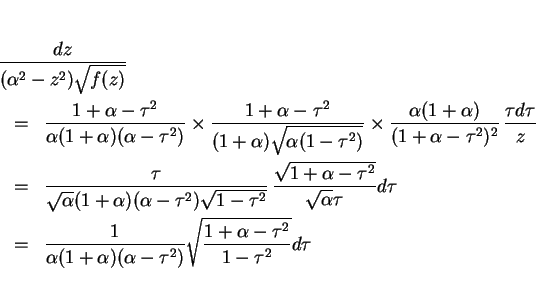
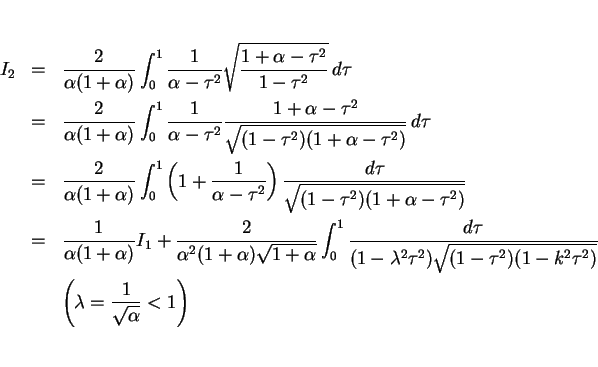
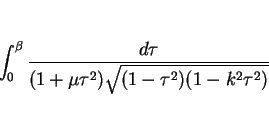
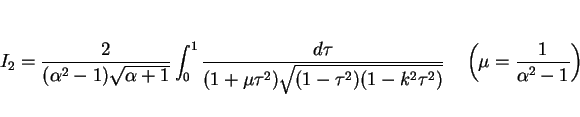
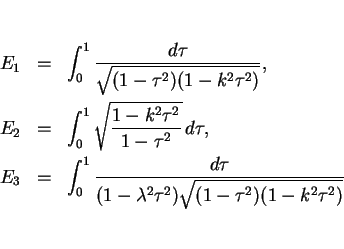
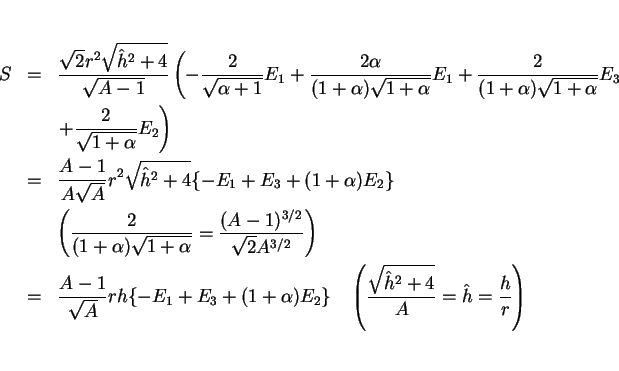
![]() と置換すれば、
根号の中が 4 次式になるので
上の計算と同様にして標準形に変換できるかも知れないが、
その 4 次式の処理は上の場合ほど簡単にはいかずかなり難しい。
しかし、多くの場合に上の場合と同様に楕円積分になってしまうであろうことは
想像がつく。
そうはならない場合については 8 節で考察する。
と置換すれば、
根号の中が 4 次式になるので
上の計算と同様にして標準形に変換できるかも知れないが、
その 4 次式の処理は上の場合ほど簡単にはいかずかなり難しい。
しかし、多くの場合に上の場合と同様に楕円積分になってしまうであろうことは
想像がつく。
そうはならない場合については 8 節で考察する。