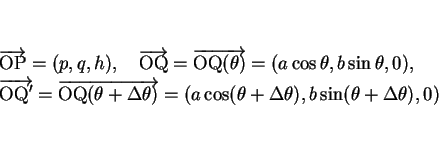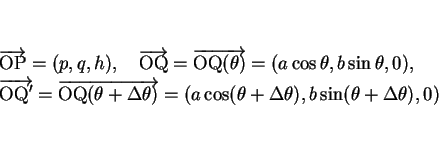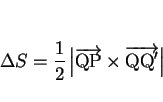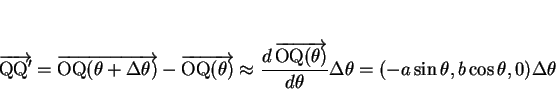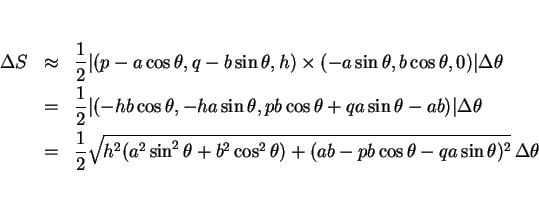

Next: 7 この積分の計算可能性
Up: 斜円錐の側面積について
Previous: 5 曲面積を求める公式:
(PDF ファイル: yokoyama1.pdf)
6 曲面積を求める公式: その 2
次は、2 節で述べた方針 3.
の方針で考える。
に対し、
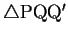 の面積を
の面積を 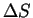 とし、
とし、
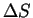 の
の 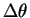 による一次近似式を求める。
による一次近似式を求める。
であるが、
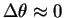 のとき
のとき
なので、
なので、この 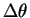 の係数を 0 から
の係数を 0 から 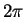 まで積分すれば
結局 (17) と同じ式が得られることになる。
まで積分すれば
結局 (17) と同じ式が得られることになる。


Next: 7 この積分の計算可能性
Up: 斜円錐の側面積について
Previous: 5 曲面積を求める公式:
Shigeharu TAKENO
2005年 2月 28日