

Next: 3 問題の定式化
Up: 斜円錐の側面積について
Previous: 1 はじめに
(PDF ファイル: yokoyama1.pdf)
2 問題
元の問題は以下のようなものであった。
問題 1
半径 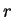 の円の円周上のある点の真上の高さ
の円の円周上のある点の真上の高さ 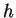 のところに
頂点があるような斜円錐 (図 1) の側面積
のところに
頂点があるような斜円錐 (図 1) の側面積 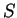 は、
通常の底面の円の中心の真上に頂点がある場合 (直円錐) の側面積に対する公式
は、
通常の底面の円の中心の真上に頂点がある場合 (直円錐) の側面積に対する公式
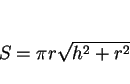 |
(1) |
で求めて構わないか
もちろん直円錐の場合はこの式 (1) で良いことはすぐに分かる。
側面は展開すれば半径
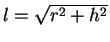 の円の一部 (扇形) で、
弧の長さは底面の円周
の円の一部 (扇形) で、
弧の長さは底面の円周 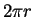 に等しい。よって、
に等しい。よって、
となる。
一方で、頂点が中心の上にない斜円錐の場合の展開図は単純ではない。
この場合、それを表す式の導き方として、次の 3 通りが考えられる。
- 側面を展開して、その扇形に似た図の中心 (元の斜円錐の頂点) から
周囲 (元の斜円錐の底面の縁) までの距離
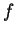 を、中心角
を、中心角 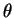 の式
の式
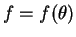 で表し (直円錐の場合は
で表し (直円錐の場合は
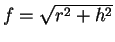 )、
)、
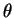 の変化の範囲
の変化の範囲
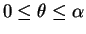 を求めて、
極座標での面積表示公式
を求めて、
極座標での面積表示公式
によって求める (図 2)。
- 底面の円周上の点を
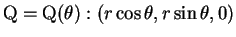 (
(
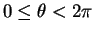 )
とパラメータ表示し、頂点 P と Q を結ぶ線分 PQ を
)
とパラメータ表示し、頂点 P と Q を結ぶ線分 PQ を
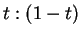 (
(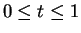 ) に内分する点を R とすることにより
側面上の任意の点 R を
) に内分する点を R とすることにより
側面上の任意の点 R を 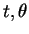 の
2 つのパラメータで表し、
パラメータで表された曲面の面積を求める面積分公式
の
2 つのパラメータで表し、
パラメータで表された曲面の面積を求める面積分公式
によって求める (図 3)。
- 区分求積の考え方に従い、底面の円周上に分点
 (
(
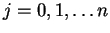 )
を取り
)
を取り
により求める (図 4)。
この場合は、
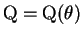 ,
,
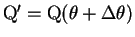 に対して
に対して
 の面積
の面積 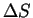 を
を
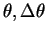 で表し、
で表し、
とすると
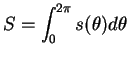 となるので、
となるので、
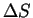 の
の 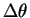 に対する 1 次近似式を求めれば良い。
に対する 1 次近似式を求めれば良い。
![\includegraphics[width=0.3\textwidth]{tenkaizu1.eps}](img35.gif)
|
![\includegraphics[width=0.3\textwidth]{mensekibun1.eps}](img36.gif)
|
![\includegraphics[width=0.3\textwidth]{kubun1.eps}](img37.gif)
|
|
図 2:
側面の展開図
|
図 3:
パラメータ表示
|
図 4:
区分求積
|
直円錐の例からすると、
1. の考え方が一番素直そうに感じるかも知れないが、
我々 (少なくとも私) の感覚では 1. が一番難しい。
それは、展開図の中心角を計ることが厄介そうだからである。
それに比べて、方針の 2., 3. は
先は長くてもとりあえずやればできそうなのでむしろ易しそうに見える。
よって実際の式の導出にはこの 2.,
3. の手法を用いることにする。
なお、誤解しやすいが、
この問題の斜円錐は直円錐を斜めに切り取ってそれを横に置いたもの
(図 5) とはならない。
それは、直円錐を斜めに切り取った面は円ではなく楕円になるからである。
実は直円錐自体は割りと易しい式で表され、
非常に古くから研究されていて色々綺麗な性質を持つので、
そういった事実が使えるかというと残念ながらそうはならない。
しかし、実際の計算では元の問題を少し一般化し、
直円錐を斜めに切り取ったものも含むようにして、
そのような場合はどうなるのかも合わせて考えることにする。


Next: 3 問題の定式化
Up: 斜円錐の側面積について
Previous: 1 はじめに
Shigeharu TAKENO
2005年 2月 28日
の円の円周上のある点の真上の高さ
のところに 頂点があるような斜円錐 (図 1) の側面積
は、 通常の底面の円の中心の真上に頂点がある場合 (直円錐) の側面積に対する公式
の円の一部 (扇形) で、 弧の長さは底面の円周
に等しい。よって、
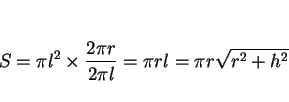
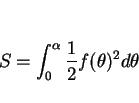
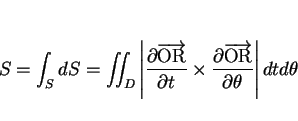
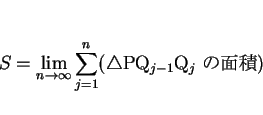
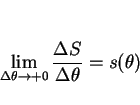
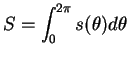 となるので、
となるので、