次へ: 7 並べ直しの具体例
上へ: sort1
前へ: 5 必要な回数の評価
(PDF ファイル: sort1-2.pdf)
6 最適解の構成
ここでは、命題 1 の十分性を与える手順を
構成することを考える。すなわち、
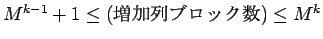 のとき、
のとき、
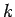 回の手順で整列化する
回の手順で整列化する
ような構成法を考える。このような構成法が見つかれば、
命題 1 より方法 A に関しては明らかにそれが最適な手順となる。
A 列の最終形の増加列ブロックが 2 つである場合をまず考える。
例えばそれが
2,3,5,1,4,6
である場合、
これは、前の (2,3,5) のブロックが 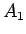 で、
後ろの (1,4,6) のブロックが
で、
後ろの (1,4,6) のブロックが 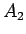 にあったはずで、
これを元の 1 増加列ブロックに直すには、
単純にそれを集めて整列化すればよい。
にあったはずで、
これを元の 1 増加列ブロックに直すには、
単純にそれを集めて整列化すればよい。
なお、この表の見方は、本来は矢印の方向に (右から左へ)
配分作業は進むのであるが、
今は A 列の最終形から A 列の初期配列に戻すということを考えているので、
それを左から右に書き表した。
以後、このような表現を用いることにする。
今度は、A 列の最終形の増加列ブロックが 3 つの場合を考える。
この場合は一つ前の段階が 2 つの増加列ブロックで、
そこからこれが作られたと考えればよい。
例えばそれが 2,3,5,4,1,6 である場合、
これは、2 回の配分後の 4 ブロックのうち一つが空集合になっていて、
例えば
であると考えれば、
と、一つ前の 2,3,4,5,1,6 の形に復元できることになる。
これは増加列ブロックが 2 つなので、
前と同じようにすれば全体を整列化できる。
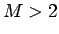 の場合も、例えば
の場合も、例えば
のように増加列ブロックが 8 つで、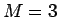 の場合、
の場合、
のようにすれば 3 個の増加列ブロックに復元できる
このようにして、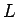 個の増加列ブロックのものを、一回戻して
個の増加列ブロックのものを、一回戻して
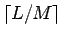 個の増加列ブロックにすることができる。
個の増加列ブロックにすることができる。
命題 3
A 列の最終列に含まれる増加列のブロック数が 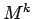 個以下ならば、
個以下ならば、
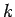 回の手順で生成でき、その手順は上のように構成可能である。
回の手順で生成でき、その手順は上のように構成可能である。
次へ: 7 並べ直しの具体例
上へ: sort1
前へ: 5 必要な回数の評価
竹野茂治@新潟工科大学
2006年2月24日
のとき、
回の手順で整列化する
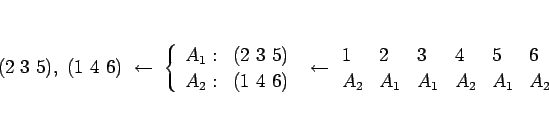
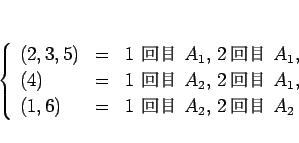
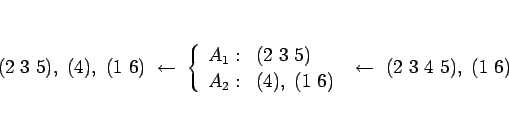
![]() の場合も、例えば
の場合も、例えば
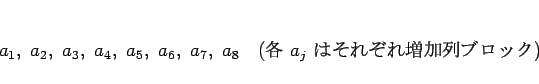
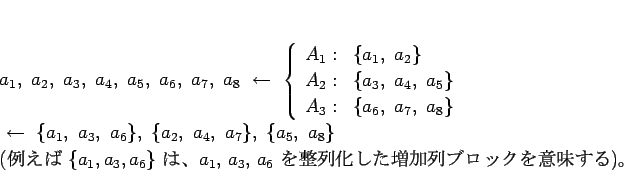
![]() 個の増加列ブロックのものを、一回戻して
個の増加列ブロックのものを、一回戻して
![]() 個の増加列ブロックにすることができる。
個の増加列ブロックにすることができる。
![]() 個以下ならば、
個以下ならば、
![]() 回の手順で生成でき、その手順は上のように構成可能である。
回の手順で生成でき、その手順は上のように構成可能である。