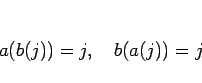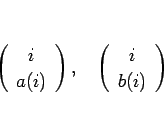次へ: 5 必要な回数の評価
上へ: sort1
前へ: 3 簡単な解
(PDF ファイル: sort1-2.pdf)
4 A 列と B 列
次に、初期配列に依存した最適解について考察する。
ここでもしばらくは 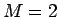 の場合の方法 A について考えることにする。
の場合の方法 A について考えることにする。
3 節同様に最初の列が 1,2,...,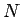 の並びであるとして
(前節のかっこのついた数字)、
この配分でどのような列が生成するかを考えることにする。
1,2,...,
の並びであるとして
(前節のかっこのついた数字)、
この配分でどのような列が生成するかを考えることにする。
1,2,...,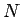 の初期配列から全ての順列が生成できれば、
逆に考えれば、全ての順列を整列化できることになる。
の初期配列から全ての順列が生成できれば、
逆に考えれば、全ての順列を整列化できることになる。
今後、この初期配列を 1,2,...,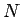 のように見る方を A 列 と呼び、
元々紙に書かれている数字の並びの方を B 列 と呼ぶこととする。
のように見る方を A 列 と呼び、
元々紙に書かれている数字の並びの方を B 列 と呼ぶこととする。
3 節の例で言えば、A 列の初期配列が 1,2,...,16 で
B 列の最終配列が 1,2,...,16 であることになる。
なお、この A 列の最後の並びを 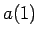 ,
,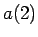 ,...,
,...,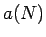 ,
B 列の初期配列を
,
B 列の初期配列を 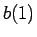 ,
,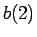 ,...,
,..., 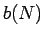 とすると、任意の
とすると、任意の 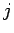 に対し
に対し
の関係があることがわかる。これは数学的には、2 つの置換
が逆置換の関係にあることを意味している。
次へ: 5 必要な回数の評価
上へ: sort1
前へ: 3 簡単な解
竹野茂治@新潟工科大学
2006年2月24日
![]() の並びであるとして
(前節のかっこのついた数字)、
この配分でどのような列が生成するかを考えることにする。
1,2,...,
の並びであるとして
(前節のかっこのついた数字)、
この配分でどのような列が生成するかを考えることにする。
1,2,...,![]() の初期配列から全ての順列が生成できれば、
逆に考えれば、全ての順列を整列化できることになる。
の初期配列から全ての順列が生成できれば、
逆に考えれば、全ての順列を整列化できることになる。
![]() のように見る方を A 列 と呼び、
元々紙に書かれている数字の並びの方を B 列 と呼ぶこととする。
のように見る方を A 列 と呼び、
元々紙に書かれている数字の並びの方を B 列 と呼ぶこととする。
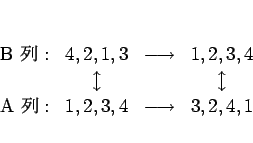
![]() ,
,![]() ,...,
,...,![]() ,
B 列の初期配列を
,
B 列の初期配列を ![]() ,
,![]() ,...,
,..., ![]() とすると、任意の
とすると、任意の ![]() に対し
に対し