次へ: 4 A 列と B 列
上へ: sort1
前へ: 2 問題設定
(PDF ファイル: sort1-2.pdf)
3 簡単な解
ここでは、まず簡単に思いつく解を一つ紹介する。
例として、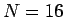 ,
, 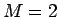 で、方法は A の場合で説明する。
で、方法は A の場合で説明する。
- 1 回目に、
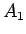 に 8 以下、
に 8 以下、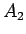 に 9 以上の番号を配り分け、
それを集める。
すると、手持ちの紙は上半分が 1 から 8, 下半分が 9 から 16 になる
(図 1)。
に 9 以上の番号を配り分け、
それを集める。
すると、手持ちの紙は上半分が 1 から 8, 下半分が 9 から 16 になる
(図 1)。
- 2 回目の分配では、
- 最初の 8 枚は、
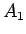 に
に 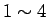 を、
を、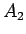 に
に 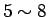 を、
を、
- 残りの 8 枚は、
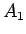 に
に 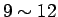 を、
を、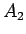 に
に 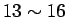 を
を
それぞれ配分する。その結果は、上から 4 枚ずつ 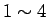 ,
,
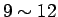 ,
, 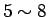 ,
, 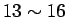 と分けられることになる
(図 2)。
と分けられることになる
(図 2)。
- 3 回目、4 回目も同様に、それぞれの小ブロックを、
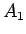 には小さい数、
には小さい数、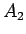 には大きい数となるように 2 つに分けて
分配していく
(図 3)。
その結果、4 回目にすべて 1 枚ずつのブロックに分割され、
上から順に、
には大きい数となるように 2 つに分けて
分配していく
(図 3)。
その結果、4 回目にすべて 1 枚ずつのブロックに分割され、
上から順に、
と並ぶことになる。
この最後の並びは、最初の並びが何であっても上の手順で確実に
その並びにできる。
よって、この最後の並びが 1,2,3,..., 16 となるように
という対応をつけて逆に考え、このかっこの方の数字を紙の数字と
見ることで昇順に整列化できることになる。
例えば、上の 1 回目の配分は、
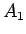 が
が 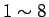 ,
, 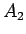 が
が 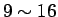 , すなわち、かっこの数字で言えば
, すなわち、かっこの数字で言えば
と分けることに相当する (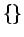 内は順不同)。
これまでの作業をこのように読み変えていけばよい。
内は順不同)。
これまでの作業をこのように読み変えていけばよい。
ついでに 2,3,4 回目の配分も書き上げると、
と、このように整列化が進むことになる。
しかし、これらの分配は人間がすぐに判定して左右に分けることは難しいので、
コンピュータの音声ガイドなどが必要であると思われる。
この方法だと、
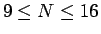 の場合は今と同じやり方で
4 回で整列化が行なえる。一般の
の場合は今と同じやり方で
4 回で整列化が行なえる。一般の 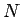 ,
, 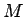 の場合は、
の場合は、
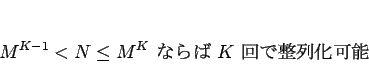 |
(1) |
となることが言え、よって必要な回数は
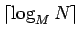 となる
(
となる
(
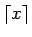 は
は 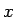 以上の最小の整数)。
以上の最小の整数)。
しかし、これはどのような初期配列に対しても同じ回数かかる手順であり、
最適な解ではない。
次へ: 4 A 列と B 列
上へ: sort1
前へ: 2 問題設定
竹野茂治@新潟工科大学
2006年2月24日
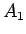 に
に 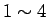 を、
を、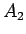 に
に 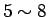 を、
を、
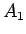 に
に 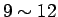 を、
を、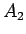 に
に 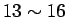 を
を
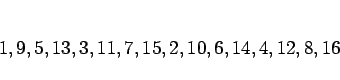
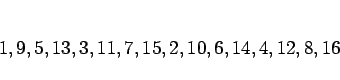
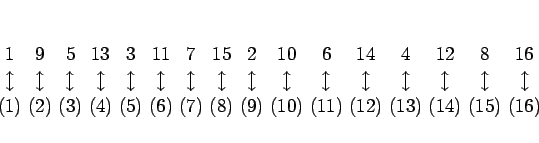
![]() が
が ![]() ,
, ![]() が
が ![]() , すなわち、かっこの数字で言えば
, すなわち、かっこの数字で言えば



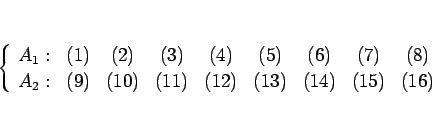
![]() の場合は今と同じやり方で
4 回で整列化が行なえる。一般の
の場合は今と同じやり方で
4 回で整列化が行なえる。一般の ![]() ,
, ![]() の場合は、
の場合は、