次へ: 3 簡単な解
上へ: sort1
前へ: 1 はじめに
(PDF ファイル: sort1-2.pdf)
2 問題設定
ここでは、問題の設定を明確にする。
それぞれに番号が書かれている 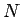 枚の紙を、
いくつかの山に適当に配り分け、
そしてそれを積み上げて再び配り分ける、
といったことを何回か繰り返すことで整列化する、ということを考える。
配ることができる場所の数を
枚の紙を、
いくつかの山に適当に配り分け、
そしてそれを積み上げて再び配り分ける、
といったことを何回か繰り返すことで整列化する、ということを考える。
配ることができる場所の数を 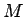 (
(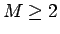 ) とし、
それらにそれぞれ
) とし、
それらにそれぞれ 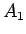 ,
, 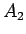 , ...,
, ..., 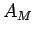 と名前をつけることにする。
と名前をつけることにする。
- ルール 1:
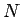 枚の紙には同じ番号が書かれたものはないとし、
よって、簡単のため、1 から
枚の紙には同じ番号が書かれたものはないとし、
よって、簡単のため、1 から 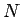 までの数が書かれているものとする。
までの数が書かれているものとする。
- ルール 2: 手持ちの紙は、上から 1 枚ずつ、
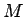 個の場所のいずれかの場所の一番上に置いていく。
個の場所のいずれかの場所の一番上に置いていく。
- ルール 3: 山に配ったものを手の方に戻したり、
配っている途中で山の紙を別の山へ移動したりはしないものとする。
- ルール 4:
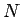 枚を配り終えたら、
枚を配り終えたら、
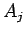 の山を順番に重ね、それを新たな手持ちの山とし、
必要ならば何回かこの操作を繰り返す。
の山を順番に重ね、それを新たな手持ちの山とし、
必要ならば何回かこの操作を繰り返す。
- ルール 5:
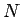 枚を配り終えるまで作業は中断しないものとし、
ルール 4 の最後の手持ちの山が整列化されることを目標とする。
枚を配り終えるまで作業は中断しないものとし、
ルール 4 の最後の手持ちの山が整列化されることを目標とする。
- ルール 6:
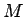 個の場所には、
紙が 1 枚も置かれない場所があってもよい。
個の場所には、
紙が 1 枚も置かれない場所があってもよい。
配り方、集め方としては、次の 2 種類を考えることとする。
- 方法 A: 山に置くときには紙を裏返して置き、
最後に集めるときは、
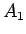 の上に
の上に 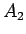 を、
を、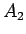 の上に
の上に 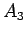 を、
という順に重ねていき、最後にそれ全体を引っくり返して手持ちとする。
すなわち、
を、
という順に重ねていき、最後にそれ全体を引っくり返して手持ちとする。
すなわち、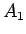 の一番下 (一番初めに配ったもの) が手持ちの一番上に、
の一番下 (一番初めに配ったもの) が手持ちの一番上に、
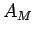 の一番上 (一番最後に配ったもの) が手持ちの一番下にくることになる。
の一番上 (一番最後に配ったもの) が手持ちの一番下にくることになる。
- 方法 B: 山に置くときには紙を表のまま置き、
最後に集めるときは、
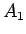 の下に
の下に 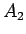 を、
を、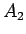 の下に
の下に 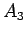 を、
という順に重ねていき、それを手持ちとする。
すなわち、
を、
という順に重ねていき、それを手持ちとする。
すなわち、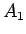 の一番上 (一番最後に配ったもの) が手持ちの一番上に、
の一番上 (一番最後に配ったもの) が手持ちの一番上に、
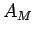 の一番下 (一番最初に配ったもの) が手持ちの一番下にくることになる。
の一番下 (一番最初に配ったもの) が手持ちの一番下にくることになる。
方法 A の方が考察には単純であるが、
実際に配るときは番号等を確認できる方法 B の方が多少便利である。
ルール 5 により、手持ちの紙を 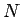 回分配する作業が単位となるので、
作業回数は、それを 1 回、と数えることにする。
よって、1 回の作業は紙の
回分配する作業が単位となるので、
作業回数は、それを 1 回、と数えることにする。
よって、1 回の作業は紙の 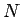 回の分配の手順からなることになる。
回の分配の手順からなることになる。
なお、[1] では、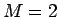 で、かつ上のルール 3、ルール 4 に対し、
で、かつ上のルール 3、ルール 4 に対し、
- ルール 3': 配っている途中で、右の山の一番上を左の山に移動したり、
左の山の一番上を右の山に移動したりしてもよい
- ルール 4': 配り終ったものを再び手に戻すことはしない (1 回で終り)
というルールの元での考察を行っているが、
実際にはルール 3' のような答案用紙の移動はやりづらいし、
そこに時間のロスが起きる。
しかも、上記のルールの場合は、機械化も可能だと思われるが、
ルール 3' の場合は機械化も複雑になると予想される。
実行に必要な手順数についても、[1] の設定よりも
このルールの方がいい結果が得られることもわかった。
次へ: 3 簡単な解
上へ: sort1
前へ: 1 はじめに
竹野茂治@新潟工科大学
2006年2月24日
![]() 枚の紙を、
いくつかの山に適当に配り分け、
そしてそれを積み上げて再び配り分ける、
といったことを何回か繰り返すことで整列化する、ということを考える。
配ることができる場所の数を
枚の紙を、
いくつかの山に適当に配り分け、
そしてそれを積み上げて再び配り分ける、
といったことを何回か繰り返すことで整列化する、ということを考える。
配ることができる場所の数を ![]() (
(![]() ) とし、
それらにそれぞれ
) とし、
それらにそれぞれ ![]() ,
, ![]() , ...,
, ..., ![]() と名前をつけることにする。
と名前をつけることにする。
![]() 回分配する作業が単位となるので、
作業回数は、それを 1 回、と数えることにする。
よって、1 回の作業は紙の
回分配する作業が単位となるので、
作業回数は、それを 1 回、と数えることにする。
よって、1 回の作業は紙の ![]() 回の分配の手順からなることになる。
回の分配の手順からなることになる。
![]() で、かつ上のルール 3、ルール 4 に対し、
で、かつ上のルール 3、ルール 4 に対し、