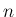
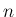 ,
, 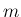 に対する
に対する 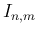 の値をいくつか紹介しておく。
の値をいくつか紹介しておく。
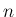 \ \ 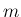 |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 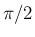 |
× | × | × | × | × | × |
| 2 | 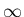 |
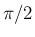 |
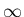 |
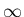 |
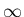 |
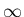 |
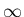 |
| 3 | 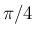 |
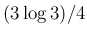 |
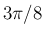 |
× | × | × | × |
| 4 | 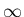 |
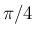 |
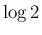 |
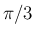 |
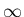 |
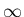 |
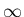 |
| 5 | 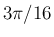 |
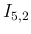 |
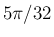 |
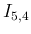 |
 |
× | × |
| 6 |  |
 |
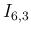 |
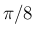 |
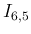 |
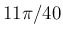 |
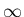 |
| 7 | 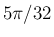 |
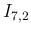 |
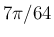 |
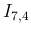 |
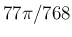 |
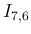 |
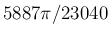 |
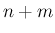 が奇数の項は、複数の対数が出てくるために長い式になる。
その上に記載されてない値は以下の通りである。
が奇数の項は、複数の対数が出てくるために長い式になる。
その上に記載されてない値は以下の通りである。
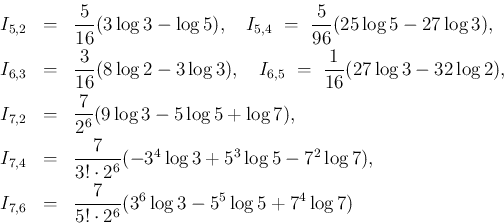
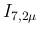 が比較的綺麗な形になっているように見えるが、
これは
が比較的綺麗な形になっているように見えるが、
これは
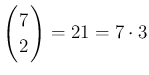
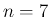 の場合だけにたまたま起こることで、
より大きい
の場合だけにたまたま起こることで、
より大きい 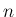 に対してはこのような形にはならない。
竹野茂治@新潟工科大学
に対してはこのような形にはならない。
竹野茂治@新潟工科大学