6 非同次の線形漸化式
最後に、非同次の定数係数線形漸化式
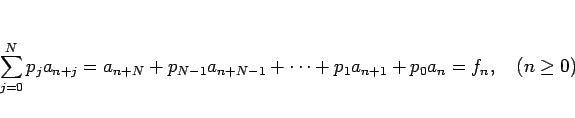 |
(29) |
(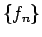 は既知の数列、
は既知の数列、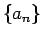 が未知の数列) についても簡単に述べておこう。
が未知の数列) についても簡単に述べておこう。
次の事実は、命題 1 と同様に容易にわかる (証明は略す)。
命題 4
非同次の漸化式 (29) の一般解は、
(29) の一つの解と、
同次の漸化式 (3) の一般解の和で表される。
これにより、(29) の一般解を求めるには、
(29) のなんらかの解 (特殊解)
を一つ求めれば良いことになるが、その解法を述べるために、
次のような記法、用語を用いることにする。
まず、非同次の漸化式 (29) に対しても、
(10) を (29) の特性方程式と呼び、
(10) の左辺を (29) の 特性多項式 と呼ぶ。
逆に、最高次数の係数が 1 で、定数項が 0 でない多項式
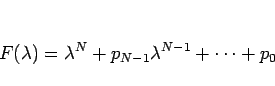
を特性多項式とする漸化式 (29) の左辺を、
この多項式 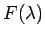 に 付随する漸化式 と呼び、
に 付随する漸化式 と呼び、
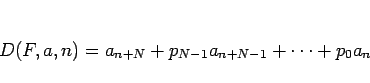
のような記号で書くことにする。
命題 5
-
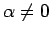 のとき、非同次漸化式
のとき、非同次漸化式
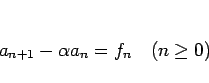 |
(30) |
の解の一つは、
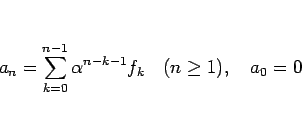 |
(31) |
で与えられる。
- (29) の特性多項式
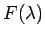 が、
最高次数の係数が 1 の 2 つの多項式
が、
最高次数の係数が 1 の 2 つの多項式 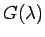 ,
, 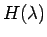 の積に
因数分解されるとき、
数列
の積に
因数分解されるとき、
数列 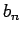 をこの
をこの 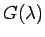 に付随する漸化式
に付随する漸化式 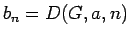 とすると、
とすると、
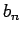 は
は 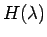 を特性多項式に持つ漸化式
を特性多項式に持つ漸化式 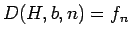 を満たす
(すなわち
を満たす
(すなわち
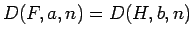 が成り立つ)。
が成り立つ)。
証明
1.
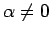 より、(30) の
より、(30) の 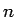 を
を 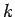 として、
その両辺を
として、
その両辺を 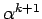 で割れば
で割れば
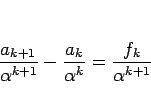
となる。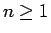 に対してこれを
に対してこれを 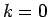 から
から 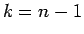 まで加えれば、
まで加えれば、
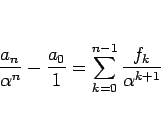
となるので、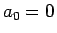 とすれば (31) が得られる。
とすれば (31) が得られる。
2.
まず、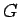 が 1 次式のときに示す。
が 1 次式のときに示す。
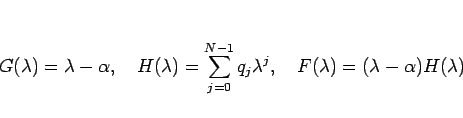
とすると、
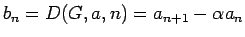 より
より
となる。一方、
となり、確かに (32) が (33) に
付随する漸化式であることがわかる。
よって (32) の右辺は 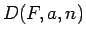 と書けるから
と書けるから
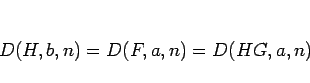 |
(34) |
が一次式の  について言えたことになる。
について言えたことになる。
 が 2 次以上の場合は、(34) を
繰り返し用いればよい。例えば
が 2 次以上の場合は、(34) を
繰り返し用いればよい。例えば  が 2 次の場合、
が 2 次の場合、
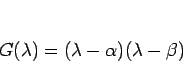
と因数分解して
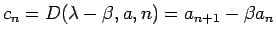 とすれば、
(34) より
とすれば、
(34) より 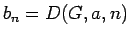 は
は
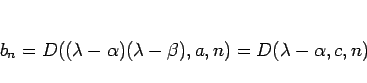
となるから、再び (34) を繰り返し使うことで
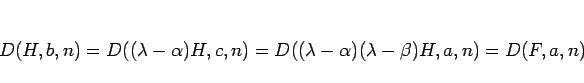
が得られる。
ここで、命題 5 の 1. の (31) の右辺は、たたみこみ と呼ばれる次の記号
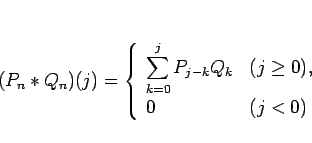
を使うと
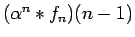 と書けることを注意しておく。
と書けることを注意しておく。
この命題 5 により、
非同次の漸化式 (29) の特殊解を求める問題は、
一つ項数の低い漸化式に帰着できることがわかる。
例えば特性多項式 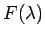 が
が
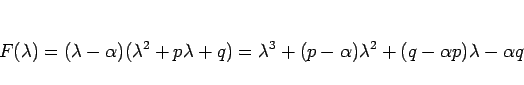
の 3 次式の場合を考えてみよう。この場合、非同次の漸化式は
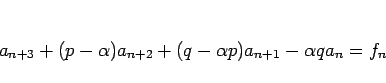 |
(35) |
となるが、命題 5 の 2. は、
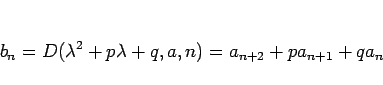 |
(36) |
とすると、(35) の左辺が
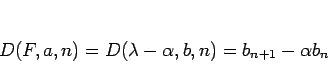 |
(37) |
となることを意味している。
なおこれは、(37) に (36) を
代入することで (35) の左辺が得られることを
直接確認することもできる。
よって、(35) は 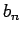 では
では
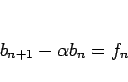
となるので、命題 5 の 1. により
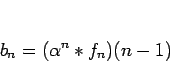 |
(38) |
がその一つの解となる。
よって、(36), (38) により
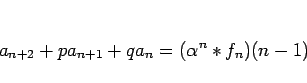 |
(39) |
となり、4 項の非同次漸化式 (35) が
3 項の非同次漸化式 (39) に帰着されることになる。
同じように
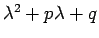 を因数分解すれば 2 項の漸化式に帰着され、
最終的に
を因数分解すれば 2 項の漸化式に帰着され、
最終的に 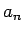 が求まることになる。
が求まることになる。
されに今の考察から、
例えば
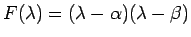 の場合、
の場合、
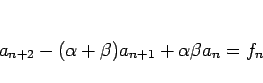 |
(40) |
の特殊解は、
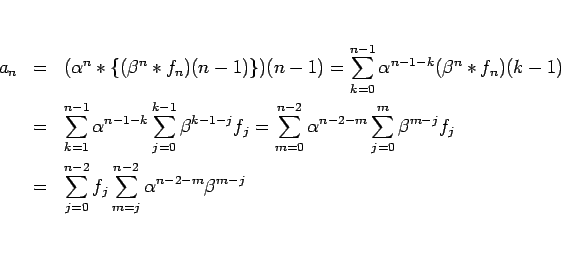
となることがわかる。
この最後の和は、
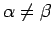 のときは等比級数で、
のときは等比級数で、
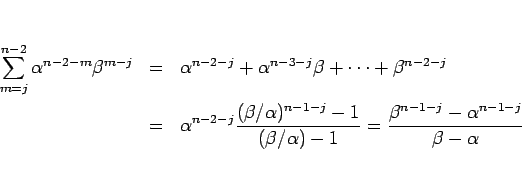
となり、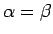 のときは定数和で、
のときは定数和で、
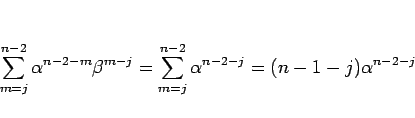
となる。
よって、(40) の 特殊解は、
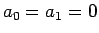 ,
,  に対しては、
に対しては、
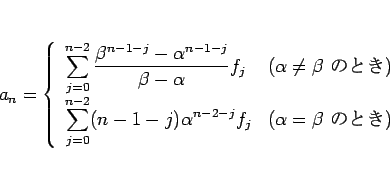
となる。
なお、高校の数学での漸化式の解法では、
特性方程式はむしろ本節のような使い方をするのが主のようで、例えば
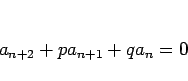
の一般項を求めるのに、
特性方程式
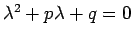 の 2 つの解
の 2 つの解 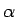 ,
, 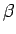 を使って、
命題 5 の 2. のような変形を行い、
を使って、
命題 5 の 2. のような変形を行い、
とし、
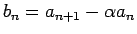 とおいて
とおいて
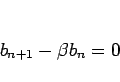
より 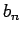 を等比数列として求め、
そこから命題 5 の 1. の
ような方法で
を等比数列として求め、
そこから命題 5 の 1. の
ような方法で 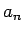 を求めること行われているようである。
を求めること行われているようである。
なお、
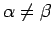 の場合は、
(41) の
の場合は、
(41) の 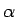 と
と 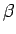 を入れかえた
を入れかえた
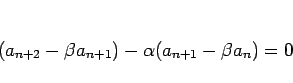
という変形を行うことで
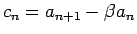 とおいて
とおいて 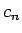 を求めることができるから
を求めることができるから
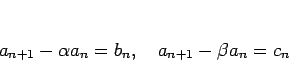
から 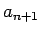 を消去して
を消去して 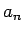 を求める、という方法もある。
を求める、という方法もある。
竹野茂治@新潟工科大学
2009年8月5日
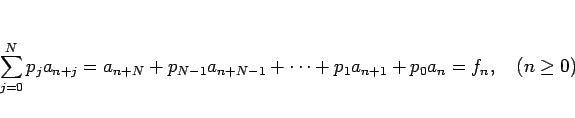
![]() より、(30) の
より、(30) の ![]() を
を ![]() として、
その両辺を
として、
その両辺を ![]() で割れば
で割れば
![]() が 1 次式のときに示す。
が 1 次式のときに示す。
![]() が 2 次以上の場合は、(34) を
繰り返し用いればよい。例えば
が 2 次以上の場合は、(34) を
繰り返し用いればよい。例えば ![]() が 2 次の場合、
が 2 次の場合、
![]() が
が
![]() では
では
![]() の場合、
の場合、
![]() の場合は、
(41) の
の場合は、
(41) の ![]() と
と ![]() を入れかえた
を入れかえた