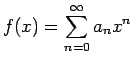 ,
,
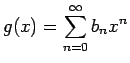 の場合、
この積は、形式的に展開すれば、
の場合、
この積は、形式的に展開すれば、
まず、
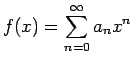 ,
,
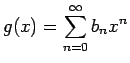 の場合、
この積は、形式的に展開すれば、
の場合、
この積は、形式的に展開すれば、
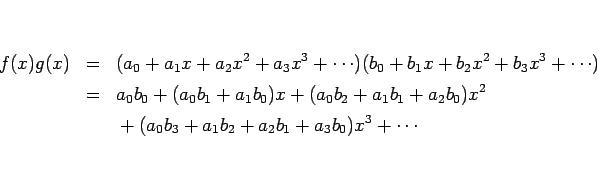
![]() の収束半径が
の収束半径が ![]() ,
, ![]() の収束半径が
の収束半径が ![]() であるとき、
であるとき、
![]() (
(![]() は
は ![]() と
と ![]() の
小さい方を意味する)
とすると、
の
小さい方を意味する)
とすると、![]() で (16) の右辺は絶対収束し、
(16) の等式が成り立つ。
で (16) の右辺は絶対収束し、
(16) の等式が成り立つ。
証明
![]() では少なくとも
では少なくとも
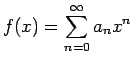 ,
,
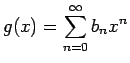 は絶対収束するから、
は絶対収束するから、
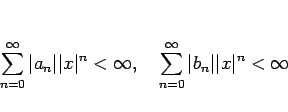
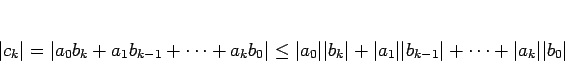
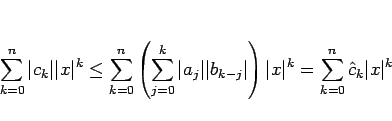
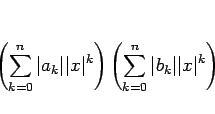
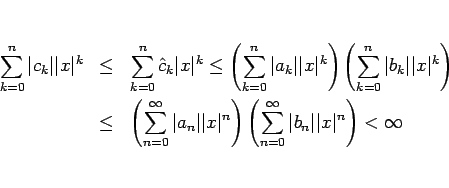
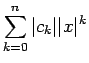 は上に有界となり、
よって
は上に有界となり、
よって
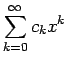 は絶対収束する。
は絶対収束する。
後は、これが ![]() に等しいことを示せばよいが、
に等しいことを示せばよいが、
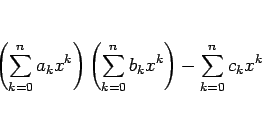
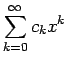 にそれぞれ収束するので、
これが
にそれぞれ収束するので、
これが
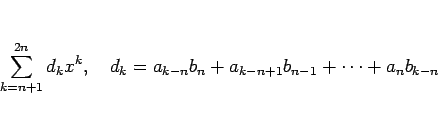
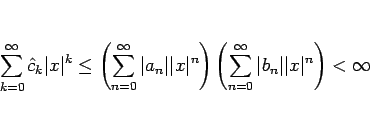
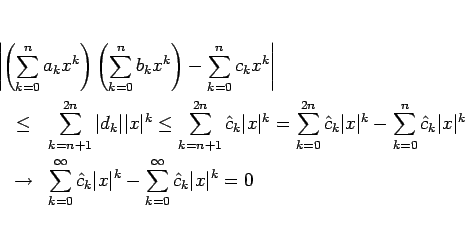
なお、この定理は、![]() が (16) の右辺の収束半径に等しい、
ということは意味しておらず、(16) の右辺の収束半径は
少なくとも
が (16) の右辺の収束半径に等しい、
ということは意味しておらず、(16) の右辺の収束半径は
少なくとも ![]() 以上であることを言うのみである。
以上であることを言うのみである。
例は後でまとめて紹介することにして、次はベキ級数の合成を考える。
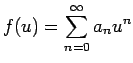 に、
に、
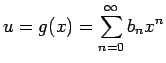 を代入してできる
ベキ級数を求める。
を代入してできる
ベキ級数を求める。
この場合、もちろん ![]() が
が ![]() の収束半径内に
入っていないといけないのであるが、
普通は
の収束半径内に
入っていないといけないのであるが、
普通は ![]() の場合、すなわち
の場合、すなわち ![]() の場合を考える。
こうであれば、
の場合を考える。
こうであれば、![]() が十分小さければ
が十分小さければ ![]() の値も十分小さくなるので
自然に
の値も十分小さくなるので
自然に ![]() の収束半径内におさまる。
逆に
の収束半径内におさまる。
逆に ![]() でない場合は、
でない場合は、
![]() の方を
の方を ![]() の代わりに
の代わりに ![]() を中心に展開して、
を中心に展開して、
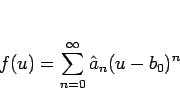
もちろん、![]() の場合でも
の場合でも ![]() の値さえ
の値さえ ![]() の収束半径内に
入っていれば代入は可能なのであるが、
それには応用上も問題がある。
それは、
の収束半径内に
入っていれば代入は可能なのであるが、
それには応用上も問題がある。
それは、![]() の収束が一番速い、
つまり有限項の近似が最もよいのは展開の中心である
の収束が一番速い、
つまり有限項の近似が最もよいのは展開の中心である ![]() の付近であり、
の付近であり、
![]() の場合も同じく
の場合も同じく ![]() の近くが最も精度がよい。
よって、合成して得られる
の近くが最も精度がよい。
よって、合成して得られる ![]() のベキ級数は、
のベキ級数は、 ![]() 、
そうでなければ
、
そうでなければ ![]() を
を ![]() を中心に展開しておく、
とすることで最も精度がよくなる。
を中心に展開しておく、
とすることで最も精度がよくなる。
よってここでは、![]() 、すなわち
、すなわち
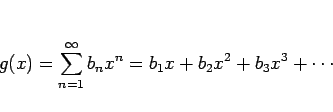
![]() を
を ![]() のベキ級数に代入すると、
のベキ級数に代入すると、
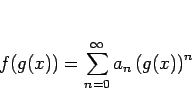
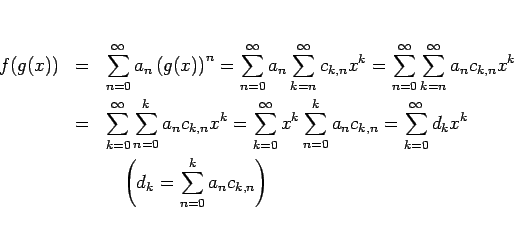
これが行える保証としての証明をちゃんと書くのは面倒なので省略するが、 結論は以下のようになる。
![]() の収束半径が
の収束半径が ![]() ,
, ![]() の収束半径が
の収束半径が ![]() であるとし、
さらに、
であるとし、
さらに、![]() (
(
![]() ) のときに
) のときに
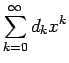 は絶対収束し、
は絶対収束し、
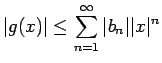 であるから、
この条件 (18) は
であるから、
この条件 (18) は ![]() よりも少し強い条件になっている。
実は、この命題の証明には、
2 重級数 (級数の級数) の順序交換を用いるのであるが、
そのときの絶対収束性の条件として、
よりも少し強い条件になっている。
実は、この命題の証明には、
2 重級数 (級数の級数) の順序交換を用いるのであるが、
そのときの絶対収束性の条件として、![]() では少し足りず、
(18) のような十分条件が必要になる。
では少し足りず、
(18) のような十分条件が必要になる。
なお、今 ![]() なので、
なので、
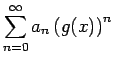 の
の ![]() 次以下の項は
次以下の項は
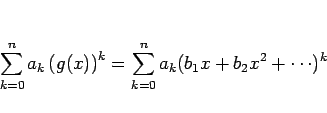
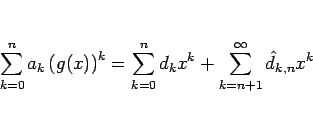
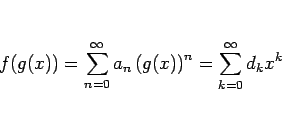
商
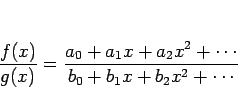
このとき、
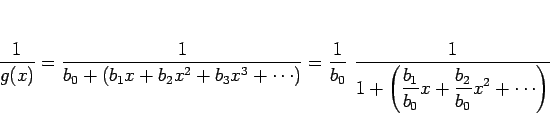
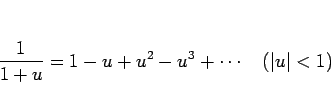
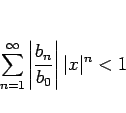
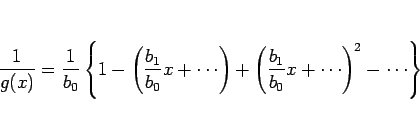
しかし、実際に商のベキ級数を計算する場合はこの方法は少し煩雑で、 以下のような方法を取ることの方が簡単である場合が多い。
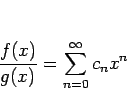
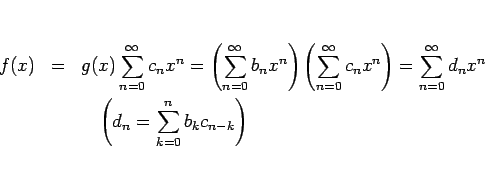
![\begin{eqnarray*}a_0 &=& b_0c_0,\\
a_1 &=& b_1c_0+b_0c_1,\\
a_2 &=& b_2c_0+b...
...lefteqn{\dotfill}
\lefteqn{\makebox[0.3\linewidth][l]{\dotfill}}\end{eqnarray*}](img337.gif)
以下に、いくつか積、合成、商の例を紹介する。
![]() の
の ![]() での展開 (4 次の項まで計算してみる)
での展開 (4 次の項まで計算してみる)
これは、
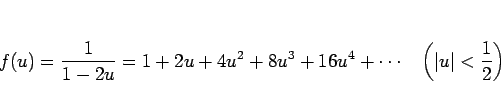
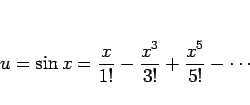
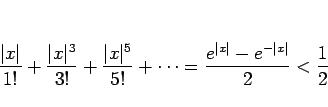
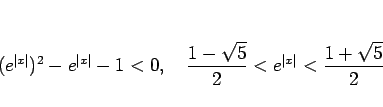
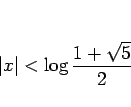
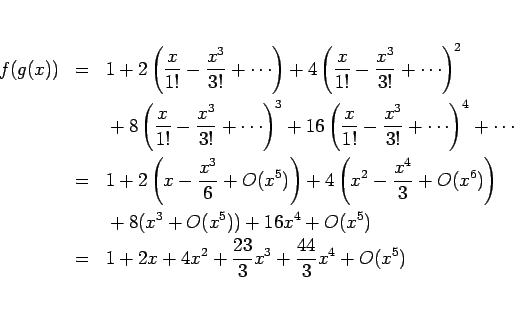
![]() の
の ![]() での展開 (5 次の項まで計算)
での展開 (5 次の項まで計算)
これは、
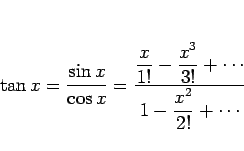
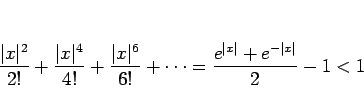
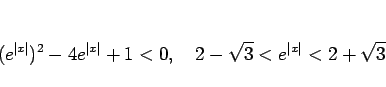
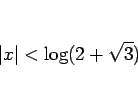
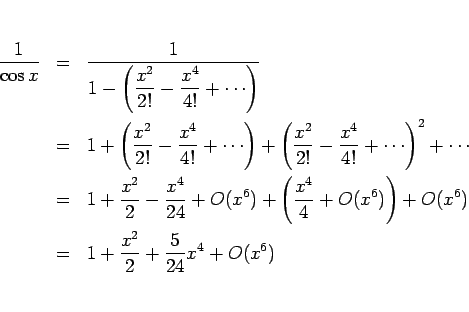
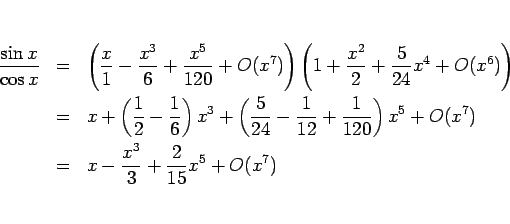
一方、第 2 の方法では次のようになる。
まず ![]() は奇関数なので、命題 16 より
偶数次の項は含まれないから、
は奇関数なので、命題 16 より
偶数次の項は含まれないから、
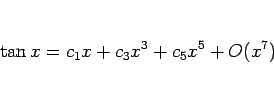
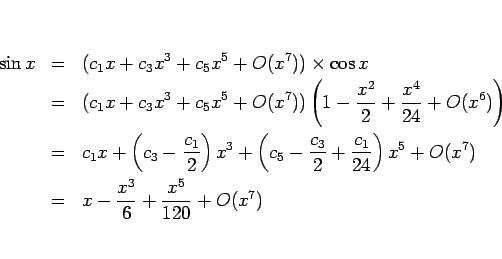
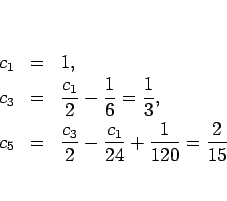
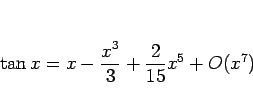
計算は明らかに後者の方が楽であろう。